Question

Find the area of the figure with the given dimensions as shown below:

 $
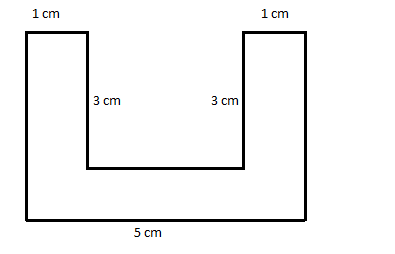
  {\text{A}}{\text{. 9 sq cm}} \\
  {\text{B}}{\text{. 10 sq cm}} \\
  {\text{C}}{\text{. 11 sq cm}} \\
  {\text{D}}{\text{. 15 sq cm}} \\
 $

Answer 1

Hint: In order to find the area of the given figure, we divide the figure into known figures for which the formula of area can be applied using the given dimensions. We divide the given figure into 3 rectangles and 2 squares and apply their formulae of area respectively.

Complete step-by-step answer:
The given figure is divided into small geometrical figures, i.e. 3 rectangles and 2 squares as shown below:

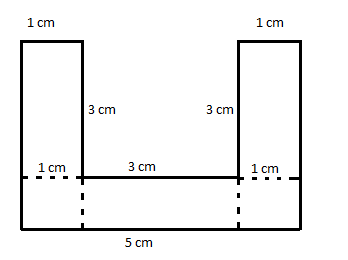
Now the total area of the figure is the sum of individual areas of each figure.
We know the area of a rectangle of length l and breadth b is given by, A = l × b.
The area of a square of side a is given by A = $ {{\text{a}}^2} $

Now from the figure we can say it formed 3 rectangles, two on the sides and one on the base of the original figure with dimensions (1 × 3), (1 × 3) and (1 × 3).
Also we formed two squares at the bottom with a side of 1 cm.
Therefore the total area of the figure is given by,
A = (1 × 3) + (1 × 3) + (1 × 3) + $ {1^2} $ + $ {1^2} $ .
⟹A = 3 + 3 + 3 + 1 + 1 = 11 sq cm.

Therefore the area of the figure is 11 sq cm.
Option C is the right answer.

Note: In order to solve this type of question the key is to exactly know how to divide the given figure into geometrical shapes by looking at the figure. Then we determine the dimensions of the geometrical figures by comparing the new figure to the original figure.
In this question we referred to the two blocks on either side of the bottom to be squares by looking at their shapes. Figures given in this type of questions like these, we consider they are drawn to scale.
Area is always represented in square units.
Sq cm can also be written as $ {\text{c}}{{\text{m}}^2} $.