Question

Find the area of the region bounded by the curve $ y = {x^2} $ and the line $ y = 4 $

Answer 1

Hint: First of all we will draw a diagram with the given conditions and data. Then will find the coordinate and then place it in the integral function and then will place a limit in it and then will simplify for the required answer.

Complete step-by-step answer:
Draw the curve with the given data where \[y = 4\] and let line AB represents \[y = 4\].
Also, $ y = {x^2} $
It can be re-written as –
Let the curve AOB represents $ {x^2} = y $

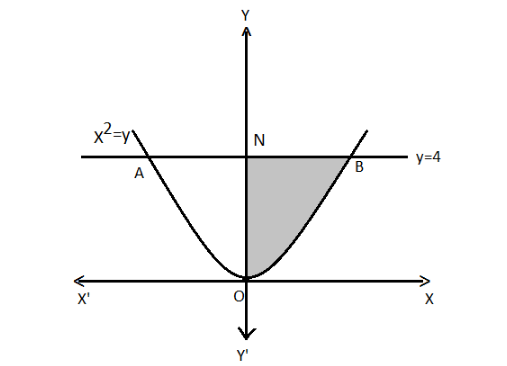
Now, the area of AOBA $ = 2 \times $ Area BONB
Place the values in the above expression –
Area $ = 2\int_0^4 x dy $ ..... (A)
We are given that –
 $ {x^2} = y $
Take square-root on both the sides of the equation –
 $ \sqrt {{x^2}} = \sqrt y $
Square and square-root cancel each other on the left hand side of the equation. Also, the square of positive and the negative term gives the positive term.
 $ \therefore x = \pm \sqrt y $
Since BONB lies in first quadrant, we have $ x = + \sqrt y $
Place the above value in the equation (A)
Area of AOBA $ = 2\int_0^4 {xdy} $
Place value for “x”
Area of AOBA $ = 2\int_0^4 {\sqrt y dy} $
It can be written as using the law of exponent.
Area of AOBA $ = 2\int_0^4 {{y^{\dfrac{1}{2}}}dy} $
Use the identity: $ \int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}} $ in the above equation.
 $ \Rightarrow A = 2\left[ {\dfrac{{{y^{\dfrac{1}{2} + 1}}}}{{\dfrac{1}{2} + 1}}} \right]_0^4 $
Simplify the above equation.
 $ \Rightarrow A = 2\left[ {\dfrac{{{y^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}}} \right]_0^4 $
Place the limit in the above equation. Lower limit is subtracted from the upper limit.
 $ \Rightarrow A = 2 \times \dfrac{2}{3}\left[ {{4^{\dfrac{3}{2}}} - 0} \right] $
Simplify the above equation.
 $ \Rightarrow A = \dfrac{4}{3}\left[ {{{(2)}^{2 \times }}^{\dfrac{3}{2}}} \right] $
Common factors from the numerator and the denominator cancels each other. Therefore remove from the numerator and the denominator.
 $ \Rightarrow A = \dfrac{4}{3}\left[ {{{(2)}^3}} \right] $
Simplify the above equation –
 $ \Rightarrow A = \dfrac{{32}}{3} $
This is the required solution.
So, the correct answer is “ $ A = \dfrac{{32}}{3} $ Sq units ”.

Note: Remember the integration identity and be careful in placing the limits. Lower limit is always subtracted from the upper limit. Refer to different laws of power and exponent to simplify the expressions.