Question

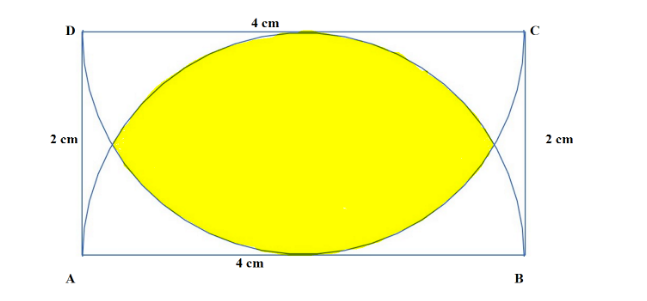
Find the area of the shaded region in the following diagram

Answer 1

Hint: Formula for area of intersection of two circle is \[A=r_{1}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{1}}}{{{r}_{1}}} \right)-{{d}_{1}}\sqrt{r_{1}^{2}-d_{1}^{2}}+r_{2}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{2}}}{{{r}_{2}}} \right)+{{d}_{2}}\sqrt{r_{2}^{2}-d_{2}^{2}}\]
Here \[{{r}_{1}}\] and \[{{r}_{2}}\] are the radius of the first and second circle.
And \[{{d}_{1}}\] , \[{{d}_{2}}\] are the distance of radius from the line that pass-through intersection of two circles.

Complete step-by-step answer:

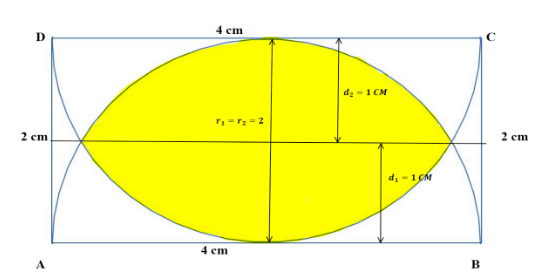
In the above diagram there are two semicircles and the semicircles are inside a rectangle.
So, we have two similar semicircles. The radius of the semi-circle is 2 centimetres. Hence here \[{{r}_{1}}=2\] and \[{{r}_{2}}=2\]. As the distance from the line intersecting two circles is one centimetre that is \[{{d}_{1}}={{d}_{2}}=1\].
Now using it in the formula for area
\[A=r_{1}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{1}}}{{{r}_{1}}} \right)-{{d}_{1}}\sqrt{r_{1}^{2}-d_{1}^{2}}+r_{2}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{2}}}{{{r}_{2}}} \right)+{{d}_{2}}\sqrt{r_{2}^{2}-d_{2}^{2}}\]
\[\Rightarrow A={{2}^{2}}{{\cos }^{-1}}\left( \dfrac{1}{2} \right)-1\sqrt{{{2}^{2}}-{{1}^{2}}}+{{2}^{2}}{{\cos }^{-1}}\left( \dfrac{1}{2} \right)+1\sqrt{{{2}^{2}}-{{1}^{2}}}\]
\[A=4{{\cos }^{-1}}\left( \dfrac{1}{2} \right)-\sqrt{3}+4{{\cos }^{-1}}\left( \dfrac{1}{2} \right)+\sqrt{3}\]
As we know \[{{\cos }^{-1}}\left( \dfrac{1}{2} \right)\]is \[\dfrac{\pi }{3}\] using this in the equation
\[\Rightarrow A=4\dfrac{\pi }{3}-\sqrt{3}+4\dfrac{\pi }{3}+\sqrt{3}=8\dfrac{\pi }{3}-0\sqrt{3}\]
Hence, the area of the shaded region is \[\left( 8\dfrac{\pi }{3} \right)c{{m}^{2}}\].

Note: Consider the following diagram

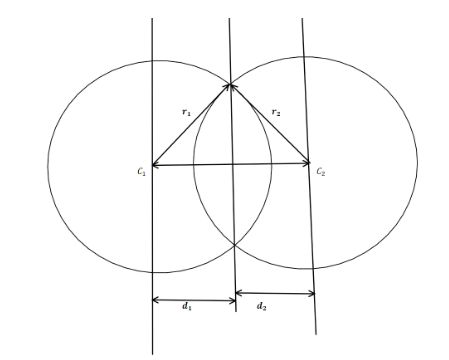
Here we have two circle with centre \[{{c}_{1}}\] and \[{{c}_{2}}\] and radius \[{{r}_{1}}\] and \[{{r}_{2}}\] and \[{{d}_{1}}\] and \[{{d}_{2}}\] are distance from the line that pass through intersection point of two circle .
And the formula for the area is
\[A=r_{1}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{1}}}{{{r}_{1}}} \right)-{{d}_{1}}\sqrt{r_{1}^{2}-d_{1}^{2}}+r_{2}^{2}{{\cos }^{-1}}\left( \dfrac{{{d}_{2}}}{{{r}_{2}}} \right)+{{d}_{2}}\sqrt{r_{2}^{2}-d_{2}^{2}}\]
This formula can be used to find the intersecting area of any two circles.