Question

Find the area of the shaded region in the following figure, where ABCD is a rectangle and all the corners are right-angled.

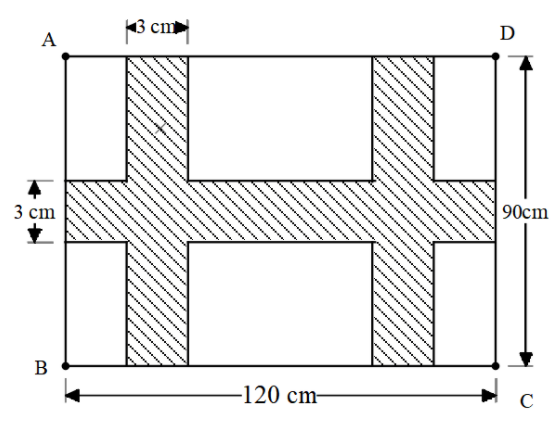
Answer 1

Hint: To solve this problem we need to find the area of horizontal and vertical strips and subtract the regions that are overlapping in the horizontal and vertical sections. The area of the rectangle is given by the product of any two adjacent sides of the rectangle. The area of a square is the just product of the side to itself.

Complete step-by-step solution:
We need to find the area of the shaded region.
The idea for this we need to find the area of the shaded region directly.
Let’s name the corners of all the unshaded portions.

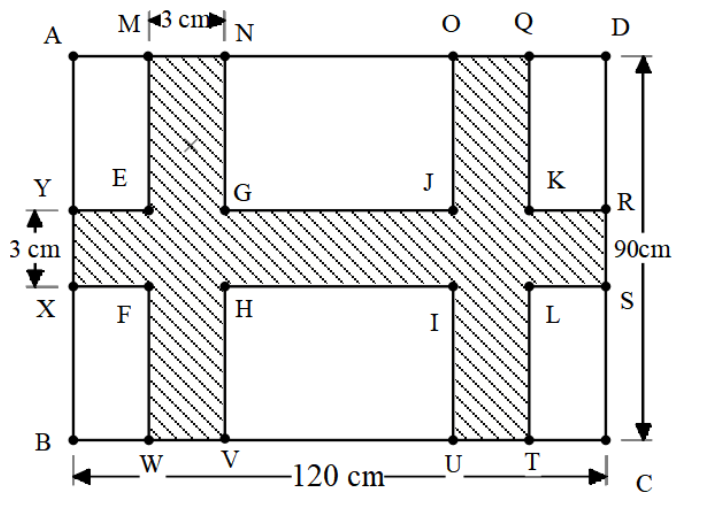
We will start by finding the area of the horizontal strip.
The area of the rectangle is equal to the product of two adjacent sides.
Therefore, the area of rectangle RSXY length is 120cm and the width is 3cm.
Therefore, the area of rectangle RSXY = $120 \times 3 = 360c{{m}^{2}}$ .
Now, we will find the area of two vertical stripes.
In rectangle MNVW, length NV is 90 cm and the width MN is 3 cm.
Therefore, the area of rectangle MNVW = $90 \times 3 = 270c{{m}^{2}}$ .
We can see that rectangle MNVW and rectangle OQTU are of the same dimensions.
 Therefore, the area of rectangle OQTU is $270c{{m}^{2}}$.
Now, we can see the strips are intersecting at the intersection we have a common area, which is calculated twice in the calculation of horizontal and vertical stripes.
The overlapping area is of square EGHF and square IJKL.
Therefore, the side of the square is 3 cm.
Therefore, the area of square EGHF = $3 \times 3 = 9c{{m}^{2}}$ .
Similarly, the area of IJKL is also $9c{{m}^{2}}$ as both the squares are of the same dimensions.
By adding all the areas of horizontal and vertical strips and subtracting the overlapping section we get,
The area of shaded region = $360 + 270 + 270 - 9 – 9$ = $882c{{m}^{2}}$.

Note: We need to keep in mind that we need to subtract the overlapping regions as they are counted twice while calculating the area of the shaded region. Also, we cannot use the second approach which is subtracting the unshaded region as the data is insufficient. It is always important to give units after every answer. And it is also important to name all the vertices as it becomes easy to solve the problems with diagrams and shapes.