Question

Find the area of the triangle using herons’ formula.

Answer 1

Hint: As we are asked to find the area of the triangle using the Herons’ formula, we first need to find the semi-perimeter s of the triangle which is equal to half of the perimeter of the triangle, i.e., $s=\dfrac{a+b+c}{2}$ , where a, b, and c are the side lengths of the triangle. Once you get the value of s, use the herons’ formula for the area of the triangle $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ to get the answer.

Complete step-by-step answer:
Let us first draw the diagram of the situation given in the question for better visualisation.

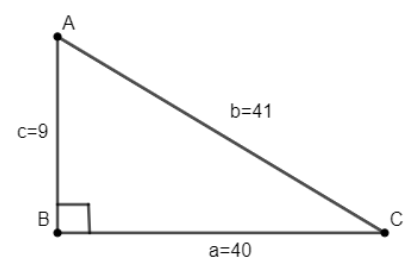
Now as we are asked to find the area of the $\Delta ABC$ using herons’ formula, we will first find the semi-perimeter s of the triangle which is equal to half of the perimeter of the triangle, i.e., $s=\dfrac{a+b+c}{2}$ . According to the figure, a=40, b=41 and c=9.
$s=\dfrac{a+b+c}{2}=\dfrac{40+41+9}{2}=45$
Now we will use the herons’ formula, according to which area of a triangle with sides a, b and c is given by $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ . Now we can substitute the known values of s, a, b and c in the formula as shown below
$\text{Area of }\Delta \text{ABC}=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}=\sqrt{45\left( 45-40 \right)\left( 45-41 \right)\left( 45-9 \right)}$
Now, we can factorise the terms inside the root for easing the calculation as below,
$\Rightarrow \text{Area of }\Delta \text{ABC}=\sqrt{45\times 5\times 4\times 36}=\sqrt{5\times 3\times 3\times 5\times 2\times 2\times 6\times 6}=5\times 3\times 2\times 6=180$
Therefore, the area of the triangle given in the question is 180 sq units.

Note: Remember that herons’ formula is valid for all the triangles with sides given. Also, if not mentioned in the question, never use herons’ formula for right angles triangles, as you can directly use the formula $area=\dfrac{1}{2}\times b\times h$ for a right angled triangle with given sides. As for the above question, base is a=40 and height is c=9. So, area is $area=\dfrac{1}{2}\times 40\times 9=180\text{uni}{{\text{t}}^{2}}$ , which is the correct answer and is easy to calculate as well.