Question

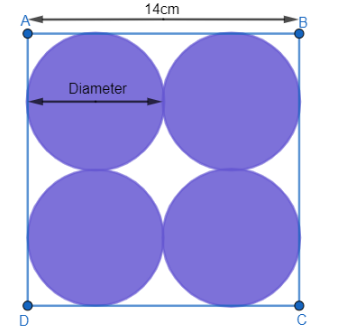
Find the area of the unshaded region in the figure, where ABCD is a square of 14 cm.

Answer 1

Hint: First of all, we should know the area of the square whose side is equal to “a” is equal to \[{{a}^{2}}\]. Now we will find the area of square ABCD whose side is equal to 14 cm. Now we should find the diameter of the circle inside the square. We know that the area of a circle whose radius is r is equal to \[\pi {{r}^{2}}\]. We also know that the diameter of the circle is equal to twice the radius. So, the area of the circle whose diameter is d is equal to \[\dfrac{\pi {{d}^{2}}}{4}\]. Now we will find the area of a circle. Now we will multiply this area with 4 to have an area of four circles inside the square ABCD. It is clear that the difference between area of square and area of four circles gives us the area of unshaded region.

Complete step-by-step answer:
Before solving the question, we should know that if the side of a square is equal to “a” then the area of the square is equal to \[{{a}^{2}}\].
From the given figure, it is clear that the side of square ABCD is equal to 14 cm.
Side of square ABCD \[=14cm\]
Area of square ABCD\[={{(14)}^{2}}c{{m}^{2}}=196c{{m}^{2}}\]

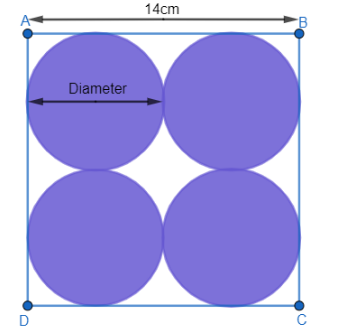
We were also given four circles in the square ABCD. Let us assume the diameter of a circle is equal to “d”. From the diagram, it is clear that the sum of diameters of two circles is equal to the side of the square.
\[\begin{align}
  & \Rightarrow 2d=14cm \\
 & \Rightarrow d=7cm.....(1) \\
\end{align}\]
So, it is clear that there are four circles in the square whose diameter is equal to 7 cm.
From the question, it is clear that we should find the area of the unshaded region.
Area of unshaded region= Area of square – Area of four circles in the square.
We know that the area of a circle whose radius is r is equal to \[\pi {{r}^{2}}\].
We know that the diameter of the circle is equal to twice the radius.
So, the area of the circle whose diameter is d is equal to \[\dfrac{\pi {{d}^{2}}}{4}\].
Now we have to calculate the area of the circle of diameter 7 cm.
So, the area of circle of diameter 7 cm \[=\dfrac{\pi {{\left( 7 \right)}^{2}}}{4}=\dfrac{49\pi }{4}\]
Now we have to calculate the area of four circles in the square ABCD.
Area of four circles of diameter 7 cm \[=4\left( \dfrac{49\pi }{4} \right)=49\pi \]
Now we have to calculate the area of the unshaded region.
Area of unshaded region = Area of square ABCD – Area of four circles of diameter 7 cm
Area of unshaded region \[=(49-49\pi )c{{m}^{2}}\]
Hence, the area of the unshaded region in the square ABCD is equal to \[(49-49\pi )c{{m}^{2}}\].

Note: Students may have a mistake at using the area of the circle. From equation (1), we will get the diameter of the circle. But some students may do wrong by assuming this as radius.
If this process is followed, then
The area of circle \[=\pi {{(7)}^{2}}=49\pi \]
So, the area of all four circles inside the square \[=4\left( 49\pi \right)=196\pi \]
Hence, the area of the unshaded region \[=49-196\pi \] which is less than zero. We know that the area of the region cannot be less than zero. So, this should be observed carefully while solving the problem.