Question

How do you find the axis of symmetry, graph and find the maximum or minimum value of the function \[f(x) = {(x + 4)^2} + 2\]?

Answer 1

Hint: We know that, \[y = a{x^2} + bx + c\] is the standard form of the equation of a parabola.
So, the equation of the axis of symmetry is \[x = \dfrac{{ - b}}{{2a}}\]
First, we change the given function into the general form.
Then comparing with the general form, we can find the axis of symmetry.

Complete Step by Step Solution:
It is given that, \[f(x) = {(x + 4)^2} + 2\]
We have to find the axis of symmetry, graph and find the maximum or minimum value of the given function.
We know that, \[y = a{x^2} + bx + c\] is the standard form of the equation of a parabola.
Now, the equation of the axis of symmetry is \[x = \dfrac{{ - b}}{{2a}}\]
The given function can be written as,
\[f(x) = {x^2} + 8x + 18\]
Comparing this equation with the general form of parabola we get,
\[a = 1,b = 8\] and \[c = 18\]
Substitute the value of \[a = 1,b = 8\] we get, the equation of the axis of symmetry is \[x = \dfrac{{ - 8}}{{2 \times 1}}\]
Simplifying we get,
\[x = - 4\]
This also gives the x co-ordinate of the vertex.
Substitute \[x = - 4\] in the given function we get,
\[f(x) = y = {( - 4)^2} + 8( - 4) + 18\]
Simplifying we get,
\[y = 2\]
We see that, \[a = 1 > 0\], which means that the graph has a minimum turning point with the arms open downwards.
The point \[( - 4,2)\] is the minimum value for the function.
The graph is:

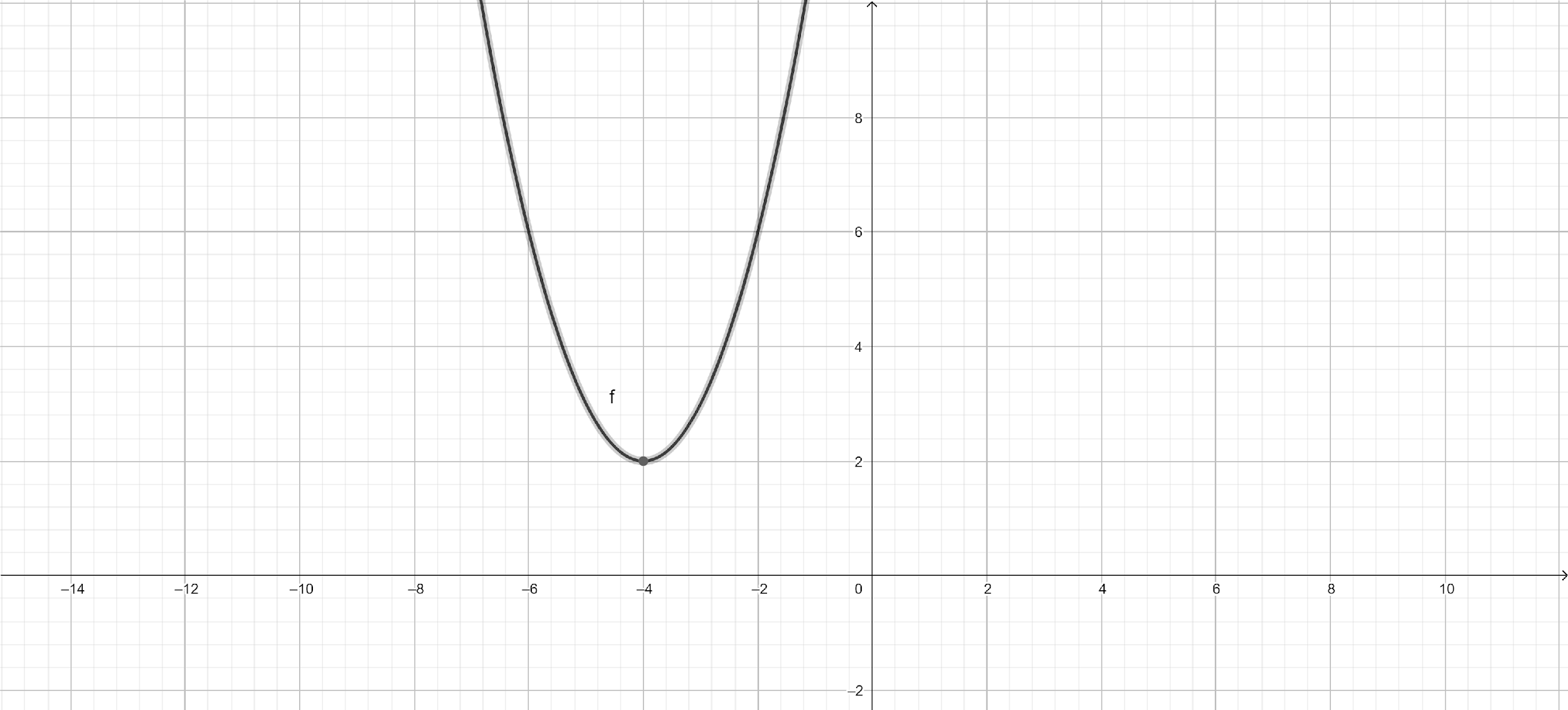
Hence, the equation of the line of symmetry is \[x = - 4\]
The point \[( - 4,2)\] is the minimum value for the function.

Note: The graph of a quadratic function is a parabola. The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves.
The axis of symmetry always passes through the vertex of the parabola . The \[x\] -coordinate of the vertex is the equation of the axis of symmetry of the parabola.
We know that, \[y = a{x^2} + bx + c\] is the standard form of the equation of a parabola.
So, the equation of the line of symmetry is \[x = \dfrac{{ - b}}{{2a}}\]
If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value.