
Find the central angle of the pie chart for winter.
Season Number of Votes Summer 90 Rainy 120 Winter 150
(a) 90
(b) 120
(c) 150
(d) None of these
| Season | Number of Votes |
| Summer | 90 |
| Rainy | 120 |
| Winter | 150 |
Answer
512.4k+ views
Hint: In this question, first of all, find the total votes by adding all three number of votes. Now, to find the central angle of any season, divide the votes of that season by total votes and multiply the ratio by
Complete step-by-step answer:
In this question, by using the following table, we have to find the central angle of winter.
We know that the pie chart is basically a type of graph in which a circle is divided into sectors that each represent a proportion of the whole.
Let us find the total number of votes. So, we get,
Total votes = (Number of votes of Summer season + (Number of votes of Rainy Season) + (Number of votes of Winter Season)
By substituting the values from the table, we get,
So, we get the central angle of each season as,
So, we get,
By substituting the total votes as 360 and votes for winter as 150, we get,
Similarly, we get the central angle of the rainy season as
Similarly, we get the central angle of the summer season as
So, now by using the central angles, we can draw the pie chart as follows.
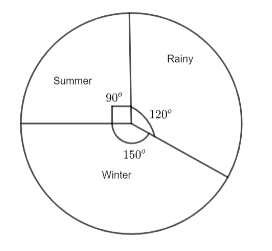
Hence, option (c) is the right answer
Note: In this question, students can verify by adding all the angles and checking if it is equal to
Complete step-by-step answer:
In this question, by using the following table, we have to find the central angle of winter.
| Season | Number of Votes |
| Summer | 90 |
| Rainy | 120 |
| Winter | 150 |
We know that the pie chart is basically a type of graph in which a circle is divided into sectors that each represent a proportion of the whole.
Let us find the total number of votes. So, we get,
Total votes = (Number of votes of Summer season + (Number of votes of Rainy Season) + (Number of votes of Winter Season)
By substituting the values from the table, we get,
So, we get the central angle of each season as,
So, we get,
By substituting the total votes as 360 and votes for winter as 150, we get,
Similarly, we get the central angle of the rainy season as
Similarly, we get the central angle of the summer season as
So, now by using the central angles, we can draw the pie chart as follows.

Hence, option (c) is the right answer
Note: In this question, students can verify by adding all the angles and checking if it is equal to
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Differentiate between the Western and the Eastern class 9 social science CBSE




