Question

Find the curved surface area of a frustum cone whose larger and smaller radius is 35 m and 10 m. The slant height is 45 m. (Use $ \pi = 3 $ )
A. $ 6,375\;{m^2} $
B. $ 6,275\;{m^2} $
C. $ 6,075\;{m^2} $
D. $ 6,175\;{m^2} $

Answer 1

Hint: The word frustum is a Latin word that means ‘piece cut off’. The lower part of the cone left after cutting a cone horizontally parallel to the base is called a frustum. Thus there are two parallel plane surfaces in a frustum and in the question we are provided with their radius. Using the formula for calculating the curved surface area of a frustum, we can find out the correct answer.

Complete step-by-step answer:

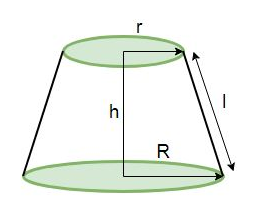
The curved surface area of a frustum is given by the formula,
 $ CSA = \pi l(R + r) $
where $ R = $ radius of the bigger circle, $ r = $ radius of the smaller circle, $ l = $ slant height of the cone.
In this question, we are given that smaller radius is 10m, $ r = 10m $
Bigger radius is 35 m, $ R = 35\;m $
And slant height is 45 m, $ l = 45\;m $
 $
   \Rightarrow CSA = 3 \times 45(35 + 10) \\
  CSA = 3 \times 45 \times 45 \\
  CSA = 6075\;{m^2} \;
  $
So curved surface area of the given frustum is $ 6075\;{m^2} $
So, the correct answer is “Option C”.

Note: The curved surface area of the frustum includes the area of only the curved surface and not that of the top and base while the total surface area includes the area of the whole frustum including the top and base.
The total surface area of the frustum is given by the formula $ TSA = \pi l(R + r) + \pi {R^2} + \pi {r^2} $
A frustum can also be made out of a pyramid. In frustum, the plane cuts parallel to the base of the frustum.