Question

How do you find the diameter of a hole?

Answer 1

Hint: In this question we have been asked to find the diameter of a hole. We will look at the various characteristics related to a hole like the radius, area and circumference and look at how we can find the value of the diameter by rearranging the terms in the formula of circumference and area. we will use the formula $circumference=\pi \times diameter$ for the circumference.

Complete step-by-step answer:
We know that a hole is a hollow place found in a rigid body or a rigid surface. The diameter is a property of a circle which tells us the length of the line which passes through the center of the circle and touches the two points on the circle on opposite sides.
A hole can be represented in the form of a circle as:

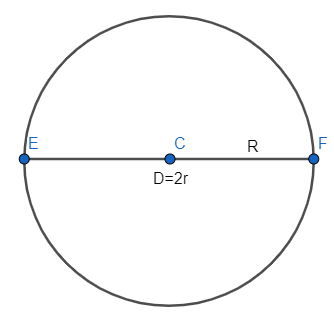
In the figure line segment $CF$ represents the radius and $EF$ represents the diameter of the circle.
We know that $d=2r$, therefore if the radius of the hole is known, then diameter can be calculated by multiplying the value by $2$.
In the case we know the circumference of a hole, we can rearrange the terms in the formula of circumference.
The formula of circumference is $circumference=\pi \times diameter$. On transferring the terms $\pi $ from the right-hand side to the left-hand side, we get:
$\Rightarrow diameter=\dfrac{circumference}{\pi }$
With this formula, we can find the diameter of the circle.

Note: It is to be remembered that a hole is also possible in a three-dimensional surface. When a hole is present in three dimensions, the hole represents a cylinder. It is also not always the case that a hole will be circular in shape. There could be holes of vague shapes for which the formulas used in the above question cannot be used.