Question

Find the diameter of the cone whose vertical angle is 60 degree and the height of the cone is 9cm?

Answer 1

Hint: The angle formed by the cone's height and slant height is known as the semi-vertical angle and it is half of the vertical angle. We also know that the tan is defined as the ratio of perpendicular and base in the right-angled triangle. We are also familiar with the value of $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$.

Complete step-by-step solution:
We have given that the height of the cone is 9 cm and the vertical angle is 60degree.
So, the angle between the height and radius is half of the vertical angle. i.e., 30degree

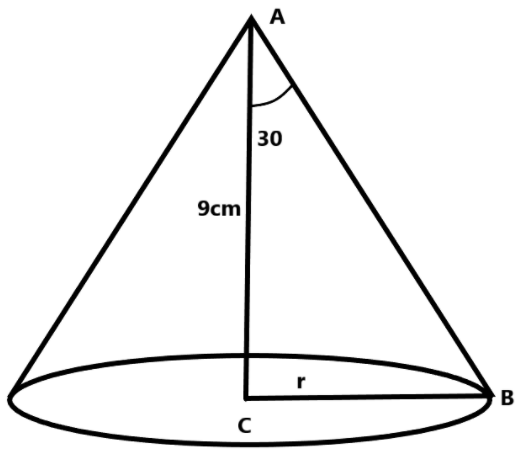
We know that the angle CAB is 30degree, we assumed the angle CAB is equal to a and the radius of the cone is equal to r.
So,
$ \Rightarrow \tan a = \dfrac{{BC}}{{AC}}$
$ \Rightarrow \tan {30^ \circ } = \dfrac{r}{9}$
We know that $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$ and substitute it
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{r}{9}$
Multiplying the both side by 9, we get
$ \Rightarrow \dfrac{9}{{\sqrt 3 }} = r$
$ \Rightarrow r = 3\sqrt 3 $
We know that the diameter is the double of radius
So,
Diameter of cone
$ = 2r$
$ = 2 \times 3\sqrt 3 $
$ = 6\sqrt 3 $
The diameter of the cone is $6\sqrt 3 $ .

Note: We should also note that the formula for calculating the slant height is \[l = \sqrt {{r^2} + {h^2}} \] if we have the values of r, h. We should also know the lateral surface area is \[S = \pi rl\] , where l is the slant height, r is radius and h is the height of the cone.