
Find the domain of
Answer
484.8k+ views
Hint: The domain of a function is the set of its possible inputs where for which the function is defined. We should remember that the base of a logarithm must be a positive number and it should not be equal to 1. The base of
Complete step-by-step solution:
Before solving question we should know that the logarithmic function
From the question, we are given a function
By comparing the function
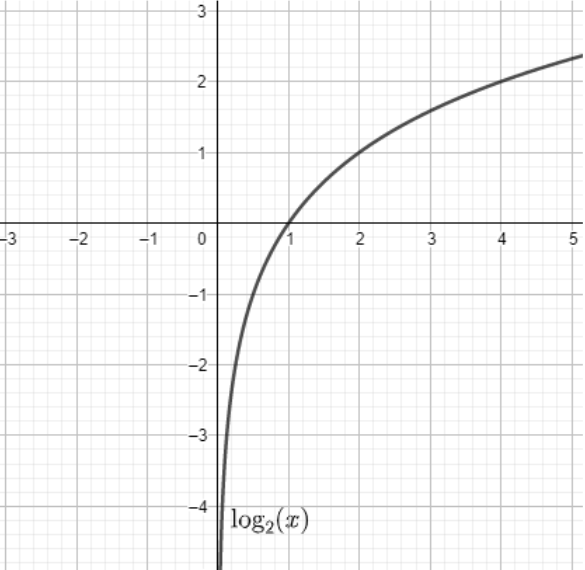
We know that for a logarithm
As the value of
The value of
The value of x should be greater than 1 and equal to zero.
So, the domain the function
Note: There is an alternative method to solve this problem. We know that the logarithmic function
2 is already greater than 0 and x must be greater than 0.
Also 2 and x must not be equal to 1. As it is clear that 2 is not equal to 1 and also x must not be equal to 1.
Combining (1) and (2) we get,
So, the domain the function
Complete step-by-step solution:
Before solving question we should know that the logarithmic function
From the question, we are given a function
By comparing the function

We know that for a logarithm
As the value of
The value of
The value of x should be greater than 1 and equal to zero.
So, the domain the function
Note: There is an alternative method to solve this problem. We know that the logarithmic function
2 is already greater than 0 and x must be greater than 0.
Also 2 and x must not be equal to 1. As it is clear that 2 is not equal to 1 and also x must not be equal to 1.
Combining (1) and (2) we get,
So, the domain the function
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Express the following as a fraction and simplify a class 7 maths CBSE

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Franz thinks Will they make them sing in German even class 12 english CBSE




