Question

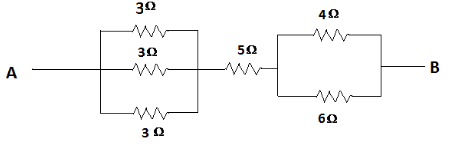
Find the equivalent resistance between points A and B

Answer 1

Hint: The 3\[\Omega \] resistors are connected in parallel to each other while the 6\[\Omega \]resistor and the 4\[\Omega \]resistor are also connected in parallel to each other. We first need to find the equivalent resistances of these resistors, and then, the equivalent resistance of these resistors is connected in series with the 5\[\Omega \] resistor.

Complete step by step answer:
Here, there are in total 6 resistors in the circuit. Of these resistors, the three 3\[\Omega \] resistors are connected in parallel with each other, while the resistors of 4\[\Omega \] and 6\[\Omega \] are also connected in parallel with each other. The equivalent resistances of these resistors are connected in series with the 5\[\Omega \] resistor.

Now, as the 3\[\Omega \] resistors are connected in parallel to each other. Thus, their voltage is constant. Thus, the equivalent resistance of these resistors would be as shown from the below formula:
\[\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}\]
\[
\Rightarrow \dfrac{1}{R'}=\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3} \\
\Rightarrow R'=1\Omega \\
\]
Now, for the resistors 4\[\Omega\]and 6\[\Omega\], the equivalent resistance would be:
\[
\dfrac{1}{R''}=\dfrac{1}{4}+\dfrac{1}{6} \\
R''=2.4\Omega \\
\]
Now, the resistors of 5\[\Omega \],2.4\[\Omega \] and the 1\[\Omega \]resistor are connected in series with each other. Thus, when the resistors are connected in series, the current between the resistors is constant. Also the current passing through the equivalent resistor would be the same as the current passing through the two resistors. The equivalent resistor of the resistors would be R, such that;
\[\therefore R = 5 + 2.4 + 1 = 8.4\Omega \]

Note: When the resistances are connected in parallel, the voltage remains constant and the net resistance is lower than the smallest resistance of the network, while when they are connected in series, the current remains constant and the net resistance is higher than the largest resistance of the network.