
Find the greatest four digit number which is a perfect square.
Answer
506.4k+ views
Hint First write the greatest four digit number and calculate its square root by long division method. After that, subtract the remainder from that number and you will get the final answer.
Complete step-by-step answer:
To find the greatest perfect square four digit number, we should know the greatest four digit number first.
The greatest four digit number = 9999
If we add the above number by one we will get a five digit number and therefore we can say that the greatest perfect square four digit number should be less than or equal to 9999.
Now if we start finding the square of the numbers randomly then it will take too much time which is not possible in exam time.
Therefore we will first find the square root of 9999 by the method of long division and if the root of the number becomes an integer then this is our required number.
To use the long division first we have to split the number in set of two numbers from right hand side to left hand side therefore we will get the number as,
99,99
Now we will use the longest division method,
\[\sqrt{9999}=9\left| \!{\overline {\,
99,99 \,}} \right. \]
I have written 9 on the outside of the sign as in this method we have to find the largest number having its square less than or equal to the first set of two numbers i.e. 99. And 9 is the largest number having square equal to 81, therefore,
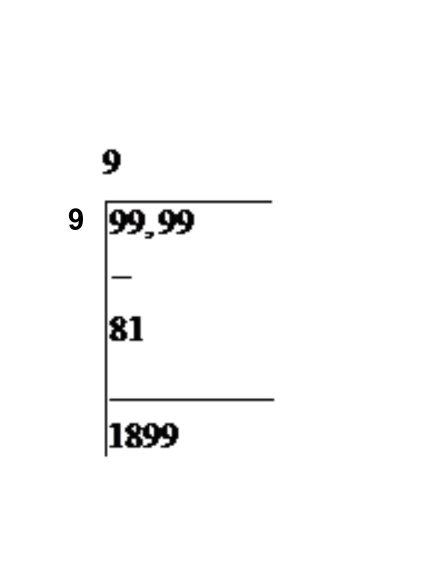
Now by using the standard operation of long division method we will get,
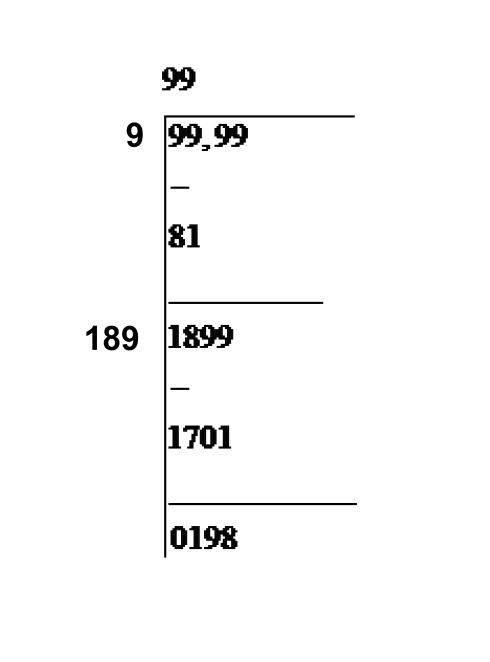
From above equation as the remainder is not equal to zero therefore the number 9999 is not a perfect square but at the same time we can say that 99 is the greatest integer number which can give a four digit square otherwise if we increase the number by one then it will become 100 and will give a six digit square.
Therefore we can say that the square of 99 is the number which gives the greatest four digits number.
Therefore,
\[{{99}^{2}}=99\times 99\]
\[\therefore {{99}^{2}}=9801\]
And therefore 9801 is the greatest four digit number which is a perfect square.
Note: In place of squaring 99 we can get the answer by just subtracting the remainder from the number we have taken for long division i.e. 9999 – 198 = 9801
Complete step-by-step answer:
To find the greatest perfect square four digit number, we should know the greatest four digit number first.
The greatest four digit number = 9999
If we add the above number by one we will get a five digit number and therefore we can say that the greatest perfect square four digit number should be less than or equal to 9999.
Now if we start finding the square of the numbers randomly then it will take too much time which is not possible in exam time.
Therefore we will first find the square root of 9999 by the method of long division and if the root of the number becomes an integer then this is our required number.
To use the long division first we have to split the number in set of two numbers from right hand side to left hand side therefore we will get the number as,
99,99
Now we will use the longest division method,
\[\sqrt{9999}=9\left| \!{\overline {\,
99,99 \,}} \right. \]
I have written 9 on the outside of the sign as in this method we have to find the largest number having its square less than or equal to the first set of two numbers i.e. 99. And 9 is the largest number having square equal to 81, therefore,
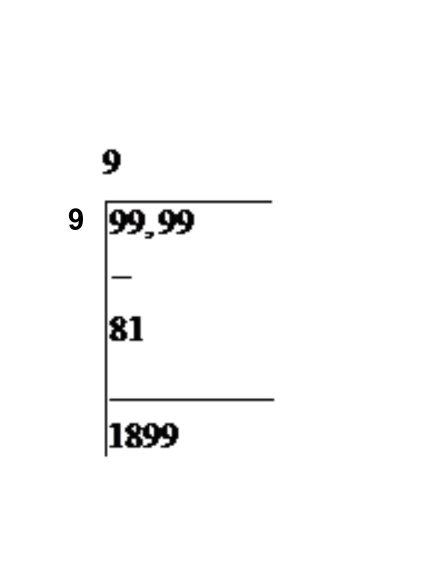
Now by using the standard operation of long division method we will get,

From above equation as the remainder is not equal to zero therefore the number 9999 is not a perfect square but at the same time we can say that 99 is the greatest integer number which can give a four digit square otherwise if we increase the number by one then it will become 100 and will give a six digit square.
Therefore we can say that the square of 99 is the number which gives the greatest four digits number.
Therefore,
\[{{99}^{2}}=99\times 99\]
\[\therefore {{99}^{2}}=9801\]
And therefore 9801 is the greatest four digit number which is a perfect square.
Note: In place of squaring 99 we can get the answer by just subtracting the remainder from the number we have taken for long division i.e. 9999 – 198 = 9801
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




