Question

Find the height of the cuboid, whose base area is 180 sq. cm and volume is 900 cu. cm.

Answer 1

Hint: A cuboid is a 3D figure which consists of 6 rectangular faces means its base is also rectangular in shape, 8 corners and 12 sides. To find the Volume of any Cuboid we use the formula:
\[\begin{gathered}
  Volume{\text{ of}}\,{\text{Cuboid}} = Length{\text{ }} \times {\text{ }}Breadth{\text{ }} \times {\text{ }}Height \\
    \\
\end{gathered} \]

Complete Step-by-step Solution

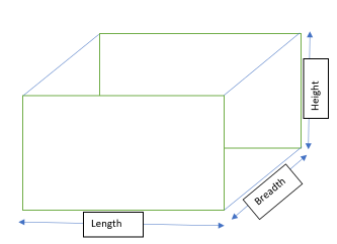
In this question we have given volume and given base area and Height of the cuboid is to be found out.
As we know volume of cuboid is Given by \[Volume{\text{ }} = {\text{ }}L \times {\text{ }}B{\text{ }} \times {\text{ }}H\] ……………. (1)
Now, as in the above fig. We are taking the base rectangular dimension as L & B.
So Base area can be given as\[\;L \times B\]
By putting the value in base area in equation (1) we get,
\[Volume{\text{ }}of{\text{ }}cuboid{\text{ }} = {\text{ }}L \times {\text{ }}B{\text{ }} \times {\text{ }}H\] …………….. (2)
As given \[Base{\text{ }}area{\text{ }} = {\text{ }}L \times B{\text{ }} = {\text{ }}180{\text{ }}square{\text{ }}cm\]
And Given \[Volume{\text{ }} = {\text{ }}900{\text{ }}cubic{\text{ }}cm\]
Now, putting these values in equation (2) we get
\[900{\text{ }} = {\text{ }}180 \times {\text{ }}H\]
So, taking 180 in the left-hand side, we get
\[H{\text{ }} = {\text{ }}900/180\] cm
So, \[H{\text{ }} = {\text{ }}5{\text{ }}cm\]

Hence the height of the cuboid equals to 5 cm.

Note: Alternative Solution:
For any Cuboid, Volume can also be given by
Volume = Base area × Height
So, Height can directly be given by \[\;Height{\text{ }} = {\text{ }}Volume/Base{\text{ }}area\]
By using this formula, we can directly find out the height of Cuboid of given base area and volume as
Height = Volume of cuboid / Base area of cuboid \[\]
So, in this given question, putting all the values of base area and volume we get
\[Height{\text{ }} = {\text{ }}900{\text{ }}/180\;\,cm\] \[ = {\text{ }}5{\text{ }}cm\]