
How do you find the inflection point of a logarithmic function?
Answer
467.1k+ views
Hint: For a function, an inflection point is a point where the curve changes its shape from concave up to concave down. We can find an inflection point by checking whether its slope at a point has the highest value than any other point. That point is called an inflection point.
Complete step by step answer:
As per the given question, we have to find the inflection points of the logarithmic function.
Let the logarithmic function be
For finding the inflection point of a logarithmic function, we need to take the derivative of the logarithmic function.
We know that the derivative of
Let
So, the first derivative which is denoted as
we can decide the inflection points based on the second derivative of the function which is given by
Here, we only require the power rule
So, the second derivative which is denoted as
If
This implies that
The graph of
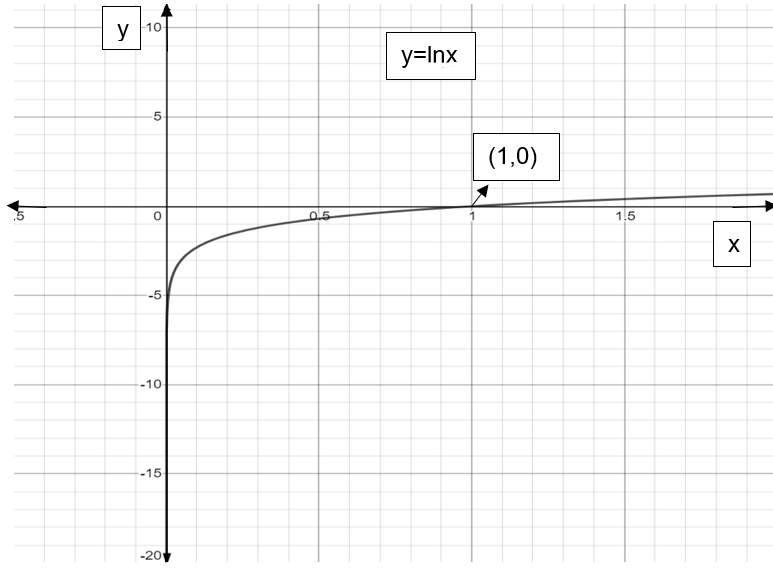
Therefore, in this way, we can find the inflection point of any logarithmic function.
Note:
In order to solve these types of problems, we must have enough knowledge about inflection points. We need to know the derivation methods to find the derivative of a function. We should avoid calculation mistakes to get the correct solution. While drawing graphs plot the points wisely to avoid any confusion.
Complete step by step answer:
As per the given question, we have to find the inflection points of the logarithmic function.
Let the logarithmic function be
For finding the inflection point of a logarithmic function, we need to take the derivative of the logarithmic function.
We know that the derivative of
Let
So, the first derivative which is denoted as
we can decide the inflection points based on the second derivative of the function which is given by
Here, we only require the power rule
So, the second derivative which is denoted as
If
This implies that
The graph of

Therefore, in this way, we can find the inflection point of any logarithmic function.
Note:
In order to solve these types of problems, we must have enough knowledge about inflection points. We need to know the derivation methods to find the derivative of a function. We should avoid calculation mistakes to get the correct solution. While drawing graphs plot the points wisely to avoid any confusion.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility

Difference between mass and weight class 10 physics CBSE

SI unit of electrical energy is A Joule B Kilowatt class 10 physics CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE




