
Find the largest number that divides 455 and 42 with the help of a division algorithm.
Answer
481.5k+ views
Hint:To solve this problem, first divide the largest number with smallest number and calculate the remainder. Then divide the divisor by the remainder and find the remainder again. Repeat this procedure till there is zero in remainder.
Complete Step-by-step solution
We know that according to Euclid’s Division Lemma if we have two positive integers a and b, then there exist unique integers q and r which satisfies the condition \[a = bq + r\;{\text{ }}\] where \[0\; \leqslant r < b\;{\text{ }}\]
i) Start with the larger integer, 455

∴\[455 = \left( {42 \times 10} \right) + 35\;\;\] (By Euclid's lemma)
Now divide 42 by 35
ii) Consider 42÷35
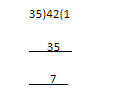
∴\[42 = \left( {35 \times 1} \right) + 7\;\;{\text{ }}\]
Now divide 35 by 7

Finally we got remainder as zero
Hence the HCF(455,42)=HCF(42,35)=HCF(35,7)=7
∴7 is the largest number that divides 455 and 42.
Additional information:
Additional information: The basis of the Euclidean division algorithm is Euclid’s division lemma. To calculate the Highest Common Factor (HCF) of two positive integers a and b we use Euclid’s division algorithm. HCF is the largest number which exactly divides two or more positive integers. That means, on dividing both the integers a and b the remainder is zero.
Note:Euclid's Division Algorithm states that the divided is equal to product of the divisor and quotient added to the remainder. Where, Quotient is denoted by q and the remainder is denoted by r. HCF * LCM = PRODUCT OF THE TWO NUMBERS
Complete Step-by-step solution
We know that according to Euclid’s Division Lemma if we have two positive integers a and b, then there exist unique integers q and r which satisfies the condition \[a = bq + r\;{\text{ }}\] where \[0\; \leqslant r < b\;{\text{ }}\]
i) Start with the larger integer, 455

∴\[455 = \left( {42 \times 10} \right) + 35\;\;\] (By Euclid's lemma)
Now divide 42 by 35
ii) Consider 42÷35
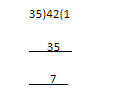
∴\[42 = \left( {35 \times 1} \right) + 7\;\;{\text{ }}\]
Now divide 35 by 7

Finally we got remainder as zero
Hence the HCF(455,42)=HCF(42,35)=HCF(35,7)=7
∴7 is the largest number that divides 455 and 42.
Additional information:
Additional information: The basis of the Euclidean division algorithm is Euclid’s division lemma. To calculate the Highest Common Factor (HCF) of two positive integers a and b we use Euclid’s division algorithm. HCF is the largest number which exactly divides two or more positive integers. That means, on dividing both the integers a and b the remainder is zero.
Note:Euclid's Division Algorithm states that the divided is equal to product of the divisor and quotient added to the remainder. Where, Quotient is denoted by q and the remainder is denoted by r. HCF * LCM = PRODUCT OF THE TWO NUMBERS
Recently Updated Pages
What percentage of the area in India is covered by class 10 social science CBSE

The area of a 6m wide road outside a garden in all class 10 maths CBSE

What is the electric flux through a cube of side 1 class 10 physics CBSE

If one root of x2 x k 0 maybe the square of the other class 10 maths CBSE

The radius and height of a cylinder are in the ratio class 10 maths CBSE

An almirah is sold for 5400 Rs after allowing a discount class 10 maths CBSE

Trending doubts
Difference between mass and weight class 10 physics CBSE

Saptarishi is the Indian name of which Constellation class 10 social science CBSE

What are the public facilities provided by the government? Also explain each facility

Complete the sentence with the most appropriate word class 10 english CBSE

What are five examples of facts and opinions class 10 english CBSE

Which state has the longest coastline in India A Tamil class 10 social science CBSE




