Question

Find the length of the diagonal of a rectangle whose sides are 6 cm and 4 cm.

Answer 1

Hint: Although all sides in a rectangle are not of equal length, they all make right angles with their consecutive sides, which results in a right-angled triangle when we draw the diagonal also. The formula that will be used here is the Pythagoras theorem.

Complete step-by-step solution:

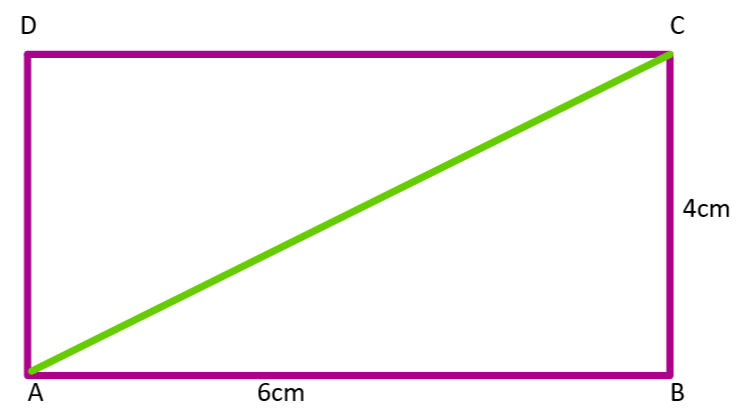
Let us assume that the given Rectangle be vertices A, B, C, D.
So the Rectangle can be taken as ABCD
Given that
The length of the sides of a rectangle is 6 cm, 4 cm.
 Therefore the length of side AB is equal to 6 cm and the length of side BC is equal to 4 cm.
$AB = 6 cm , BC = 4 cm $.
In a rectangle, we know that the length of the opposite sides is equal.
Therefore we can say that
The length of side AB is equal to the length of the side CD and the length of the side BC is equal to the length of the side DA
AB = CD = 6 cm
BC = DA = 4 cm.
In a rectangle ABCD AC and BD are diagonals.
In a rectangle, two adjacent sides always form a right angle. That is 90 degrees
Therefore,
By applying Pythagoras theorem the length of the diagonal AC is $\sqrt {A{B^2} + B{C^2}} $
$AC = \sqrt {{6^2} + {4^2}} $
$\Rightarrow AC = \sqrt {36 + 16} $
$\Rightarrow AC = \sqrt {52} $
$\Rightarrow AC = 2\sqrt {13} $ .
We know that in a rectangle the length of two diagonals is equal.
Therefore the length of the diagonal AC , BD is equal to $2\sqrt {13} $ .

Note: Never assume that answer will be in integers only. And you can remember some sets of Pythagorean triplets so that you can solve it fast during exams. Do not make calculation mistakes, make sure to check it twice.