Question

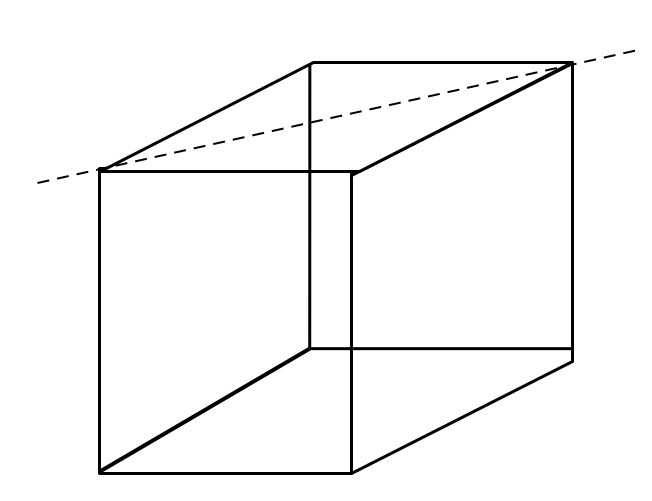
Find the moment of inertia through the face diagonal of a cube. Edge length of a cube is $a$ units.

Answer 1

Hint: The moment of inertia is however always specified with respect to the axis. We can find the moment of inertia of the cube using different equations depending upon the location of the axis.

Formula used: ${I_{tri}} = \dfrac{1}{6}M{r^2}$

Complete step by step answer:
In the given question we have been asked to find the moment of inertia through the face diagonal of a cube, the edge length of a cube is $a$ units. We know that moment of inertia is defined as property of a body undergoing rotational motion by virtue of which it resists the change in its state, i.e. it resists the torque acting on it.
According to the figure, moment of inertia of a square plate is given as,

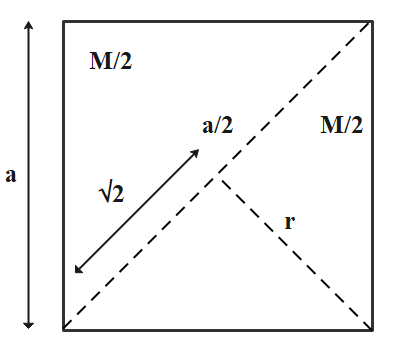
$I = 2 \times $moment of inertia of the triangular plate
We know that, Moment of inertia of the triangular plate is given as,
${I_{tri}} = \dfrac{1}{6}M{r^2}$
Now, substituting value of ${I_{tri}}$ we get,
$ \Rightarrow I = 2 \times {I_{tri}}$
$I = 2 \times \left( {\dfrac{1}{6}\dfrac{M}{2}{r^2}} \right)$
From the figure,
 $r = \sqrt {{a^2} - {{\left( {\dfrac{{\sqrt {2a} }}{2}} \right)}^2}} = \dfrac{a}{{\sqrt 2 }}$
$I = 2 \times \left( {\dfrac{1}{6}\dfrac{M}{2}{{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2}} \right)$
$ \Rightarrow I = \dfrac{{M{a^2}}}{{12}}$
Now, the cube is considered to be made up of square plates of $dm$mass stacked upon each other up to height $a$.
Thus, the moment of inertia of the cube about the diagonal can be given as,
$\int_0^I {dI} = \int_0^M {\dfrac{{{a^2}dm}}{{12}}} $
$I = \dfrac{{M{a^2}}}{{12}}$

Hence, the correct answer is $\dfrac{1}{{12}}M{a^2}$.

Note: Since, in this question the axis of rotation was at the centre, so we used the formula $\dfrac{1}{6}M{r^2}$. The perpendicular axis theorem or the parallel axis theorem can be used to determine the moment of inertia of a rigid body about any axis, if the moment of inertia about a given axis is known.