Question

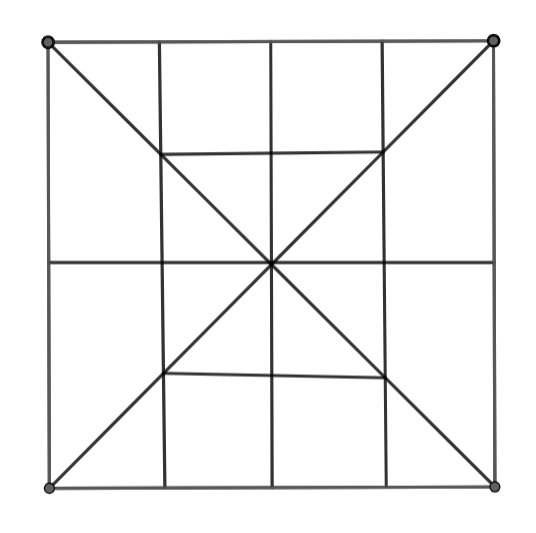
Find the number of squares in the figure given below.

Answer 1

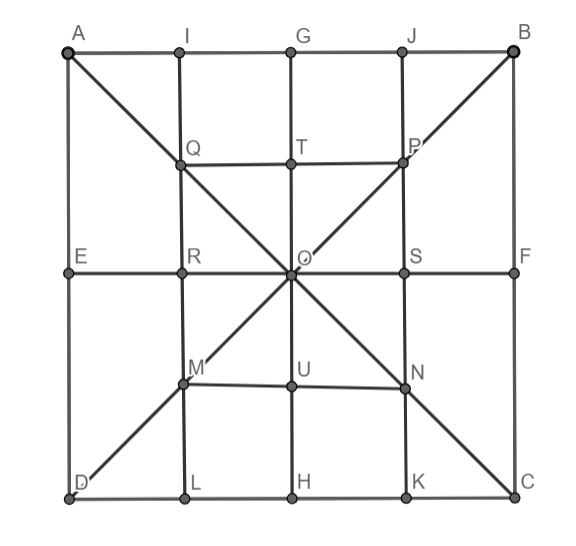
Hint: To illustrate the number of squares in the above diagram, simply list the intersection points as shown below. This will make it simple to visualize and count the required squares. We'll start with the biggest square and work our way down.

Complete step by step answer:
ABCD is the largest square containing all 20 components, and it is 1.
The 1 square that is centered and has 8 components in it is QPNM.
There are two middle-sized squares namely IJSR and RSKL which have 6 components each.
After that, we can see that there are 4 squares that have 5 components and are at the corners of the biggest square. We can name them AGOE, BGOF, CHOF, and DHOE respectively.
IGTQ, GJPT, QTOR, TPSO, ROUM, OSNU, MUHL, UNKH are the last, simplest, and smallest squares in the above figure, totaling 8 squares.
Taking this into account, we may state that the largest square is 1, the middle square is 1, the up and down squares are 2, the corner squares are 4, and the smallest squares are 8.
Now if we combine all the squares mentioned above, we will get,
$$\Rightarrow 1+1+2+4+8=16$$
So, the total number of squares in the above figure is 16 squares.

Note:
Always remember to record the points alphabetically when taking them so you don't miss any. We will only calculate the squares and ignore the rectangles and triangles that have been provided. Always start from the largest to the smallest square, or from the smallest to the largest square, to keep things simple.