Question

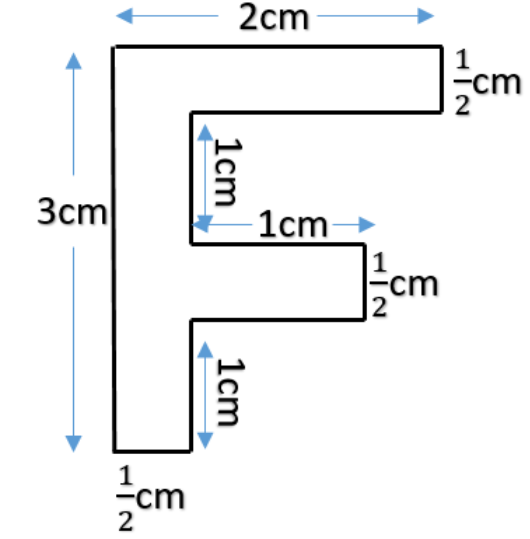
Find the perimeter of the given figure

Answer 1

Hint: Now let us first understand perimeter of objects. Now perimeter can only be defined on 2-D objects. Here when we say 2-D objects we mean 2-dimensional objects. A two-dimensional object is an object which has only length and width and no thickness. For example, a square, a rectangle, triangle, circle, and oval all are 2-dimensional objects. So what are 3-dimensional objects? Objects that we see around us are mostly 3-dimensional objects.

Complete step-by-step solution:
It has length, width as well as height or thickness.
Examples of 3-dimensional objects are cube, cylinder, sphere, etc.
Now we know that perimeter is defined for 2 Dimensional objects.
Let us try to understand what the perimeter is.
Now perimeter is nothing but the length around the objects. Hence it the length of the border of the object.
For example, let us consider a square with side 2cm

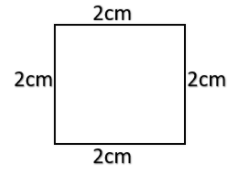
Now here the perimeter of the square will be the length of the border
Hence perimeter = $2 + 2 + 2 + 2 = 8cm.$
Hence perimeter of the square is $8 cm.$
Now consider the given figure.
Let us name the figure for understanding.

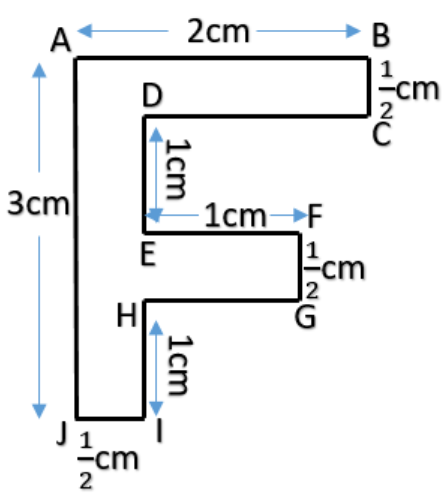
Now here perimeter = $AB + BC + CD + DE + EF + FG + GH + HI + IJ + JA.$
Now we have $AB = 2cm, JA = 3cm, DE = EF = HI =1cm$ and $BC=FG=IJ=\dfrac{1}{2}cm$
Now let us find $HG$ and $CD.$
Now from the figure, we can see that $EF = HG.$ Hence we get $HG = 1cm.$
Now also from the figure, we have $AB = CD + IJ$
Hence $2cm = CD + \dfrac{1}{2}$ hence we get CD = $2-\dfrac{1}{2}$
Now again consider perimeter = $AB + BC + CD + DE + EF + FG + GH + HI + IJ + JA.$
Substituting the values we get perimeter as
 $\begin{align}
  & =3+2+\dfrac{1}{2}+2-\dfrac{1}{2}+1+1+\dfrac{1}{2}+1+1+\dfrac{1}{2} \\
 & =3+2+2+1+1+1+1+\dfrac{1+1}{2} \\
 & =11+\dfrac{2}{2} \\
 & =11+1 \\
 & =12cm \\
\end{align}$
Hence we have perimeter of given figure is 12cm.

Note: Note that while calculating perimeter we have to take all sides just once. Students can make silly mistakes by either taking one side twice or by not counting one side by mistake. Also remember that unit of perimeter is m or cm and not \[{{m}^{2}}\] or $c{{m}^{2}}$ .