Question

How do you find the point of intersection of diagonals?

Answer 1

Hint: The diagonals of a quadrilateral are the line segments that connect opposite vertices. We will investigate the simplest case which is quadrilateral. The number of vertices in a quadrilateral are 4, and the number of diagonals are 2. To find the point of intersection of diagonals can be found using the coordinates of vertices of a quadrilateral.

Complete step-by-step solution:
We are not given a particular type of quadrilateral, let’s see the most general case with four vertices. Let the quadrilateral ABCD have coordinates of vertices as \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)\And \left( {{x}_{4}},{{y}_{4}} \right)\] respectively.

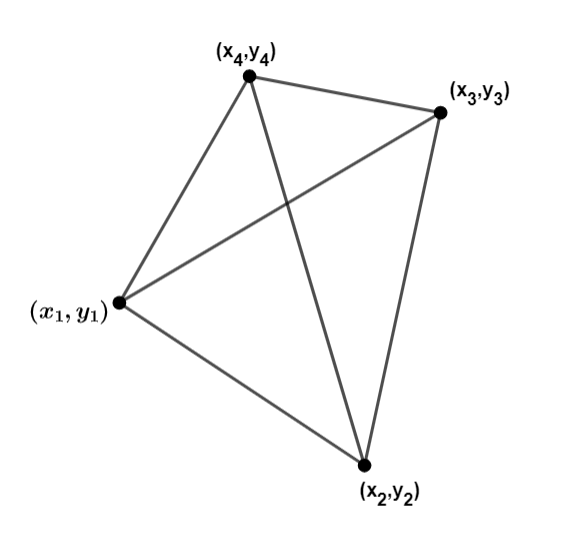
We can find the point of intersection of diagonals by writing their equation and solving both.
The equation for first diagonal is \[\dfrac{y-{{y}_{3}}}{x-{{x}_{3}}}=\dfrac{{{y}_{1}}-{{y}_{3}}}{{{x}_{3}}-{{x}_{3}}}\] , similarly the equation for the other diagonal is \[\dfrac{y-{{y}_{2}}}{x-{{x}_{2}}}=\dfrac{{{y}_{4}}-{{y}_{2}}}{{{x}_{4}}-{{x}_{2}}}\]. As the point of intersection lies on both diagonals, it must satisfy both equations. Solving the above two equations, we can find the point of intersection of diagonals.

Now, let’s look at some general cases of quadrilaterals such as square, rectangle, rhombus, parallelogram. For these quadrilaterals, the diagonals are bisectors of each other, so we can find the point of intersection by finding the midpoint of two opposite vertices.

Note: For different polygons, if the number of vertices that is the number of diagonals is more than two. We have to follow the same method, write an equation for any two diagonals, find their point of intersection, and then check if this point lies on another diagonal or not. Calculation mistakes while solving the equations should be avoided.