Question

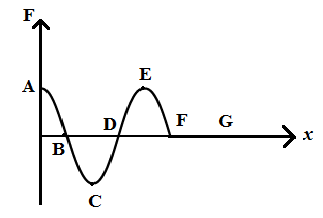
Find the positions of unstable equilibrium.

A. B
B. D
C. F
D. A

Answer 1

Hint: The particle can be said to be in unstable equilibrium if it has positive value of potential energy and it is said to be in stable equilibrium if it has negative value of potential energy. Use the relation between potential and force with respect to distance from the mean position and rearrange it for the potential energy term. In the above figure, the force is given by the cosine function.

Formula used:
\[F = - \dfrac{{dU}}{{dx}}\]
Here, U is the potential energy and x is the distance from the mean position.

Complete step by step answer:
We know that the particle can be said to be in unstable equilibrium if it has positive value of potential energy and it is said to be in stable equilibrium if it has negative value of potential energy.
We have the relation between force and potential energy with respect to the distance from the mean position as follows,
\[F = - \dfrac{{dU}}{{dx}}\]
Here, U is the potential energy and x is the distance from the mean position.
We integrate the above equation as follows,
\[U = - \int F dx\] …… (1)
From the given curve we can observe that the force is given by the cosine function as it does not start from the mean position and path difference is \[\dfrac{\pi }{2}\].
Therefore, we can write, \[F = \cos x\].
We substitute \[F = \cos x\] in the above equation.
\[U = - \int {\cos x} \,dx\]
 \[ \Rightarrow U = - \sin x + C\]
Here, C is the constant of integration. We ignore it for the ease in simplification.
From the above equation, the potential energy is positive if \[\sin x\] is negative. When we take a look at the figure, the coordinates of points A, B, C, D, E and F are\[0,\dfrac{\pi }{2},\pi ,\dfrac{{3\pi }}{2},2\pi ,\,{\text{and }}\dfrac{{5\pi }}{2}\].
We know that \[\sin x\] is negative at \[\dfrac{{3\pi }}{2}\]. Therefore, we can say that the particle has positive potential energy at \[x = D = \dfrac{{3\pi }}{2}\]. Thus, the point of unstable equilibrium is D.

So, the correct answer is option (B).

Note:
On the potential energy curve, the points lying on the curve above the mean position towards the positive y-axis are the points of unstable equilibrium and that of below the mean position are the points with stable equilibrium. In the case of unstable equilibrium, the body will not come back to its stable position. One can think of stable equilibrium as a particle on the bottom of a parabolic curve and unstable equilibrium as a particle on top of a hill curve.