
Answer
486k+ views
Hint: The range of \[{\tan ^{ - 1}}\theta \] is between \[\left. {\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right.} \right)\]. From the trigonometric table find the value of\[\left( { - \dfrac{1}{{\sqrt 3 }}} \right)\]. Now substitute this back into our given expression and simplify it to get the principal value.
Complete step-by-step answer:
A principal value of a function is the value selected at a point in the domain of a multiple-valued function, chosen so that the function has a single value at the point. The principal value of \[{\tan ^{ - 1}}\theta \]
The principal value of \[{\tan ^{ - 1}}\theta \] branches to,
\[{\tan ^{ - 1}}x \in \left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)\].
Hence the principal value of the given function will be between the range\[\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)\] .
Now we have been given the function, \[{\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right)\].
Let us first find the value of \[\left( { - \dfrac{1}{{\sqrt 3 }}} \right)\] from the above expression. By using the trigonometric table we can find the tangent function related to \[\left( { - \dfrac{1}{{\sqrt 3 }}} \right)\] . Let us draw the trigonometric table to make the identification of the function easier.
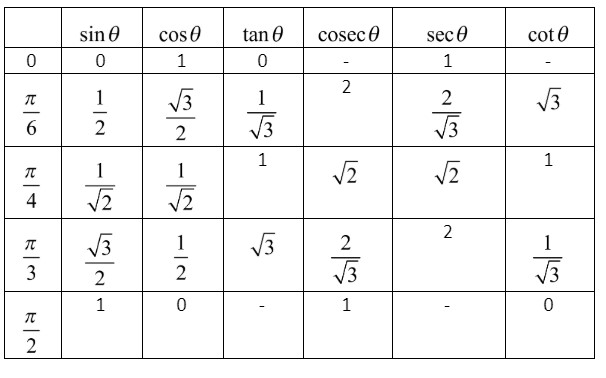
From the table we get that, \[\tan \dfrac{\pi }{6} = \dfrac{1}{{\sqrt 3 }}\].
In case of an inverse tangent function, \[{\tan ^{ - 1}}( - \theta ) = - \theta \]. Hence we get,
\[\tan \left( { - \dfrac{\pi }{6}} \right) = \left( { - \dfrac{1}{{\sqrt 3 }}} \right)\]
Now let us substitute \[\tan \left( { - \dfrac{\pi }{6}} \right)\]in the place of \[\left( { - \dfrac{1}{{\sqrt 3 }}} \right)\].Thus we can change the given expression as,
\[{\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = {\tan ^{ - 1}}\left( {\tan \left( { - \dfrac{\pi }{6}} \right)} \right)\]
Now let us simplify the above expression to get the principal value.
\[
{\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = {\tan ^{ - 1}}\left( {\tan \left( { - \dfrac{\pi }{6}} \right)} \right) \ \\
{\tan ^{ - 1}}\left( {\tan \left( { - \dfrac{\pi }{6}} \right)} \right) = \left( { - \dfrac{\pi }{6}} \right) \ \\
{\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = \left( { - \dfrac{\pi }{6}} \right) \ \\
\]
Thus we got the principal value of the given inverse tangent function as, \[\left( { - \dfrac{\pi }{6}} \right)\].
\[\therefore {\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = \left( { - \dfrac{\pi }{6}} \right)\].
Note: To solve a question like these you should be familiar with the domain and range of the sine functions as well as the domain and range of the inverse sine functions. For us the range of inverse tangent function is \[\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)\] and the domain of inverse function of tangent is \[\left( { - \infty ,\infty } \right)\]. Students should remember the important trigonometric ratios and standard angles to solve these types of questions.
Complete step-by-step answer:
A principal value of a function is the value selected at a point in the domain of a multiple-valued function, chosen so that the function has a single value at the point. The principal value of \[{\tan ^{ - 1}}\theta \]
The principal value of \[{\tan ^{ - 1}}\theta \] branches to,
\[{\tan ^{ - 1}}x \in \left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)\].
Hence the principal value of the given function will be between the range\[\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)\] .
Now we have been given the function, \[{\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right)\].
Let us first find the value of \[\left( { - \dfrac{1}{{\sqrt 3 }}} \right)\] from the above expression. By using the trigonometric table we can find the tangent function related to \[\left( { - \dfrac{1}{{\sqrt 3 }}} \right)\] . Let us draw the trigonometric table to make the identification of the function easier.

From the table we get that, \[\tan \dfrac{\pi }{6} = \dfrac{1}{{\sqrt 3 }}\].
In case of an inverse tangent function, \[{\tan ^{ - 1}}( - \theta ) = - \theta \]. Hence we get,
\[\tan \left( { - \dfrac{\pi }{6}} \right) = \left( { - \dfrac{1}{{\sqrt 3 }}} \right)\]
Now let us substitute \[\tan \left( { - \dfrac{\pi }{6}} \right)\]in the place of \[\left( { - \dfrac{1}{{\sqrt 3 }}} \right)\].Thus we can change the given expression as,
\[{\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = {\tan ^{ - 1}}\left( {\tan \left( { - \dfrac{\pi }{6}} \right)} \right)\]
Now let us simplify the above expression to get the principal value.
\[
{\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = {\tan ^{ - 1}}\left( {\tan \left( { - \dfrac{\pi }{6}} \right)} \right) \ \\
{\tan ^{ - 1}}\left( {\tan \left( { - \dfrac{\pi }{6}} \right)} \right) = \left( { - \dfrac{\pi }{6}} \right) \ \\
{\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = \left( { - \dfrac{\pi }{6}} \right) \ \\
\]
Thus we got the principal value of the given inverse tangent function as, \[\left( { - \dfrac{\pi }{6}} \right)\].
\[\therefore {\tan ^{ - 1}}\left( { - \dfrac{1}{{\sqrt 3 }}} \right) = \left( { - \dfrac{\pi }{6}} \right)\].
Note: To solve a question like these you should be familiar with the domain and range of the sine functions as well as the domain and range of the inverse sine functions. For us the range of inverse tangent function is \[\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)\] and the domain of inverse function of tangent is \[\left( { - \infty ,\infty } \right)\]. Students should remember the important trigonometric ratios and standard angles to solve these types of questions.
Recently Updated Pages
A particle is undergoing a horizontal circle of radius class 11 physics CBSE

A particle is thrown vertically upwards with a velocity class 11 physics CBSE

A particle is rotated in a vertical circle by connecting class 11 physics CBSE

A particle is projected with a velocity v such that class 11 physics CBSE

A particle is projected with a velocity u making an class 11 physics CBSE

A particle is projected vertically upwards and it reaches class 11 physics CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE




