
Answer
408k+ views
Hint: We can resolve the initial velocity and velocity at a certain point on trajectory into their horizontal and vertical components. Then by using basic trigonometric relations between the components, we can find the required answer.
Step by step solution:
When an object is thrown with some initial velocity and is allowed to fall freely under the effect of gravity of earth, then the object follows a curved path. The object is known as a projectile while this type of motion exhibited by an object under gravity is called the projectile motion.
When a projectile is projected with some initial velocity u then as it moves along its path, its velocity keeps changing and is not fixed at u.
In this question, we have a particle which is projected with a velocity u and makes an angle
$\theta $ with the horizontal. Diagrammatically, we have the following scenario.
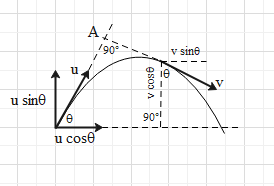
We can resolve the initial velocity into its horizontal and vertical components. We are given that at every point of trajectory, the velocity v of the particle perpendicular to its initial velocity which is represented in the diagram by reproducing the directions of u and v meeting at 90$^\circ $
at point A.
Like u, we can resolve the components of v as shown. Now we see that horizontal components of u and v must be equal. Therefore, we can write the following expression for the particle.
${\text{v sin}}\theta = u\cos \theta $
Rearranging the terms, we get the required answer to be
$
{\text{v}} = u\dfrac{{\cos \theta }}{{\sin \theta }} \\
\Rightarrow {\text{v}} = u\cot \theta \\
$
Hence, the correct answer is option C
Note: The velocity of the projectile keeps changing along its trajectory. As the projectile rises above the ground, its velocity keeps on decreasing. At the highest point v=0. As the projectile starts falling, v starts increasing but final velocity is zero as projectile comes to rest when it completes its trajectory.
Step by step solution:
When an object is thrown with some initial velocity and is allowed to fall freely under the effect of gravity of earth, then the object follows a curved path. The object is known as a projectile while this type of motion exhibited by an object under gravity is called the projectile motion.
When a projectile is projected with some initial velocity u then as it moves along its path, its velocity keeps changing and is not fixed at u.
In this question, we have a particle which is projected with a velocity u and makes an angle
$\theta $ with the horizontal. Diagrammatically, we have the following scenario.

We can resolve the initial velocity into its horizontal and vertical components. We are given that at every point of trajectory, the velocity v of the particle perpendicular to its initial velocity which is represented in the diagram by reproducing the directions of u and v meeting at 90$^\circ $
at point A.
Like u, we can resolve the components of v as shown. Now we see that horizontal components of u and v must be equal. Therefore, we can write the following expression for the particle.
${\text{v sin}}\theta = u\cos \theta $
Rearranging the terms, we get the required answer to be
$
{\text{v}} = u\dfrac{{\cos \theta }}{{\sin \theta }} \\
\Rightarrow {\text{v}} = u\cot \theta \\
$
Hence, the correct answer is option C
Note: The velocity of the projectile keeps changing along its trajectory. As the projectile rises above the ground, its velocity keeps on decreasing. At the highest point v=0. As the projectile starts falling, v starts increasing but final velocity is zero as projectile comes to rest when it completes its trajectory.
Recently Updated Pages
A particle is undergoing a horizontal circle of radius class 11 physics CBSE

A particle is thrown vertically upwards with a velocity class 11 physics CBSE

A particle is rotated in a vertical circle by connecting class 11 physics CBSE

A particle is projected with a velocity v such that class 11 physics CBSE

A particle is projected with a velocity u making an class 11 physics CBSE

A particle is projected vertically upwards and it reaches class 11 physics CBSE

Trending doubts
Find the value of the expression given below sin 30circ class 11 maths CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

In the tincture of iodine which is solute and solv class 11 chemistry CBSE

On which part of the tongue most of the taste gets class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

Who is the leader of the Lok Sabha A Chief Minister class 11 social science CBSE




