
Answer
456.6k+ views
Hint: This is the case of projectile motion where the particle is projected with some angle to the horizontal. The acceleration acting on the projectile is only in a vertical direction because gravity will be acting only in the vertical direction and along horizontal direction, there is no force. The formulas we have for horizontal range and maximum height are used here.
Formula used:
$\eqalign{
& R = \dfrac{{{u^2}\sin 2\theta }}{g} \cr
& H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}} \cr} $
$\sin 2\theta = 2\sin \theta \cos \theta $
Complete step-by-step solution:
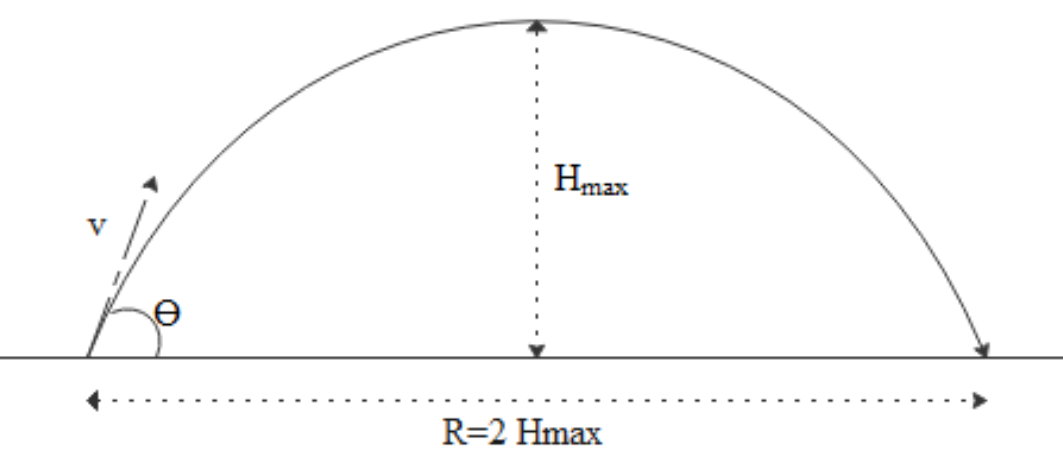
When a particle is projected with some angle to the horizontal then that particle will have both horizontal displacement and vertical displacement. Since there will be no force along the horizontal direction the velocity along the horizontal direction will be the same throughout its motion while there is a force along the vertical direction so velocity along the vertical direction will vary.
The maximum horizontal displacement a projectile can have is called the range and the maximum vertical displacement the projectile can have is called the maximum height.
The range is given with formula $R = \dfrac{{{u^2}\sin 2\theta }}{g}$ where ‘u’ is the initial velocity and $\theta $ is the angle made by the velocity with horizontal and ‘g’ is the acceleration due to gravity.
Maximum height is given by $H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ where ‘u’ is the initial velocity and $\theta $ is the angle made by the velocity with horizontal and ‘g’ is the acceleration due to gravity.
It is given that $R = 2H$. By substituting the formulas we have we will get
$R = 2H$
$ \Rightarrow \dfrac{{{u^2}\sin 2\theta }}{g} = \dfrac{{2{u^2}{{\sin }^2}\theta }}{{2g}}$
$\eqalign{
& \Rightarrow \sin 2\theta = 2\sin \theta \cos \theta \cr
& \Rightarrow \dfrac{{{u^2}2\sin \theta \cos \theta }}{g} = \dfrac{{2{u^2}{{\sin }^2}\theta }}{{2g}} \cr
& \Rightarrow \tan \theta = 2 \cr
& \Rightarrow \sin \theta = \dfrac{2}{{\sqrt 5 }} \cr
& \Rightarrow \cos \theta = \dfrac{1}{{\sqrt 5 }} \cr} $
After getting tangent value we can get sinusoidal and cosecant value because from tangent value we have opposite side and adjacent side, we have to apply pythagoras theorem to get the hypotenuse and from that we can get sin and cos values.
Now substitute those sin and cos values in range formula.
$\eqalign{
& R = \dfrac{{{u^2}2\sin \theta \cos \theta }}{g} \cr
& \Rightarrow R = \dfrac{{{u^2}2(\dfrac{2}{{\sqrt 5 }})(\dfrac{1}{{\sqrt 5 }})}}{g} \cr
& \Rightarrow R = \dfrac{{4{u^2}}}{{5g}} \cr} $
In the question initial velocity is given as ‘v’ hence answer will be $R = \dfrac{{4{v^2}}}{{5g}}$
Option A will be the correct answer.
Note: The formulas which we have are applicable only if the acceleration due to gravity is constant and not varying. We can find maximum height too as they had given the relation between maximum height and the horizontal range.
Formula used:
$\eqalign{
& R = \dfrac{{{u^2}\sin 2\theta }}{g} \cr
& H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}} \cr} $
$\sin 2\theta = 2\sin \theta \cos \theta $
Complete step-by-step solution:

When a particle is projected with some angle to the horizontal then that particle will have both horizontal displacement and vertical displacement. Since there will be no force along the horizontal direction the velocity along the horizontal direction will be the same throughout its motion while there is a force along the vertical direction so velocity along the vertical direction will vary.
The maximum horizontal displacement a projectile can have is called the range and the maximum vertical displacement the projectile can have is called the maximum height.
The range is given with formula $R = \dfrac{{{u^2}\sin 2\theta }}{g}$ where ‘u’ is the initial velocity and $\theta $ is the angle made by the velocity with horizontal and ‘g’ is the acceleration due to gravity.
Maximum height is given by $H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ where ‘u’ is the initial velocity and $\theta $ is the angle made by the velocity with horizontal and ‘g’ is the acceleration due to gravity.
It is given that $R = 2H$. By substituting the formulas we have we will get
$R = 2H$
$ \Rightarrow \dfrac{{{u^2}\sin 2\theta }}{g} = \dfrac{{2{u^2}{{\sin }^2}\theta }}{{2g}}$
$\eqalign{
& \Rightarrow \sin 2\theta = 2\sin \theta \cos \theta \cr
& \Rightarrow \dfrac{{{u^2}2\sin \theta \cos \theta }}{g} = \dfrac{{2{u^2}{{\sin }^2}\theta }}{{2g}} \cr
& \Rightarrow \tan \theta = 2 \cr
& \Rightarrow \sin \theta = \dfrac{2}{{\sqrt 5 }} \cr
& \Rightarrow \cos \theta = \dfrac{1}{{\sqrt 5 }} \cr} $
After getting tangent value we can get sinusoidal and cosecant value because from tangent value we have opposite side and adjacent side, we have to apply pythagoras theorem to get the hypotenuse and from that we can get sin and cos values.
Now substitute those sin and cos values in range formula.
$\eqalign{
& R = \dfrac{{{u^2}2\sin \theta \cos \theta }}{g} \cr
& \Rightarrow R = \dfrac{{{u^2}2(\dfrac{2}{{\sqrt 5 }})(\dfrac{1}{{\sqrt 5 }})}}{g} \cr
& \Rightarrow R = \dfrac{{4{u^2}}}{{5g}} \cr} $
In the question initial velocity is given as ‘v’ hence answer will be $R = \dfrac{{4{v^2}}}{{5g}}$
Option A will be the correct answer.
Note: The formulas which we have are applicable only if the acceleration due to gravity is constant and not varying. We can find maximum height too as they had given the relation between maximum height and the horizontal range.
Recently Updated Pages
A particle is undergoing a horizontal circle of radius class 11 physics CBSE

A particle is thrown vertically upwards with a velocity class 11 physics CBSE

A particle is rotated in a vertical circle by connecting class 11 physics CBSE

A particle is projected with a velocity v such that class 11 physics CBSE

A particle is projected with a velocity u making an class 11 physics CBSE

A particle is projected vertically upwards and it reaches class 11 physics CBSE

Trending doubts
Find the value of the expression given below sin 30circ class 11 maths CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

In the tincture of iodine which is solute and solv class 11 chemistry CBSE

On which part of the tongue most of the taste gets class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

Who is the leader of the Lok Sabha A Chief Minister class 11 social science CBSE




