
Find the square root of the number 6400.
Answer
423.8k+ views
Hint: A square root of a number is a value that, when multiplied by itself gives the number. We will use the long division method to find the square root of 6400. It is noted that the multiplication of the obtained number with itself will be equal to 6400.
Complete step-by-step answer:
It is given in the question that we have to find the square root of the number, 6400. We will use the long division method to find out the square root of 6400. For that, we must first know what square root of a number is. A square root of a number is a value which when multiplied by itself gives the number. The symbol of square root is, $\sqrt{{}}$ which means the positive square root.
Now, we will see the steps for the long division method in order to find the square root.
Step 1: Group the digits in pairs, starting with the unit place. The group number and the remaining digits, if any is called period.
Step 2: Divide with the largest number whose square root is equal to or less than the first period. Take the number as the divisor and also as the quotient.
Step 3: Subtract the product of the divisor and the quotient from the first period to the right of the remainder, this will become the dividend for the next step.
Step 4: The new divisor will be obtained by taking two times the quotient.
Step 5: Repeat steps 2, 3 and 4 till all the periods have been taken. The quotient obtained is the required square root.
Now, by keeping all the steps discussed above in mind, let us find the square root of the number, 6400.
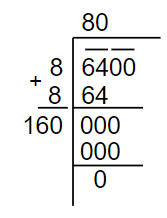
Therefore, the square root of 6400 is 80. It can be represented as $\sqrt{6400}=80$.
Thus, option (b) is the correct answer.
Note: We can also find the square root of 6400 using an alternative method called the prime factorization method, which is as follows.
$\begin{align}
& 2\left| \!{\underline {\,
6400 \,}} \right. \\
& 2\left| \!{\underline {\,
3200 \,}} \right. \\
& 2\left| \!{\underline {\,
1600 \,}} \right. \\
& 2\left| \!{\underline {\,
800 \,}} \right. \\
& 2\left| \!{\underline {\,
400 \,}} \right. \\
& 2\left| \!{\underline {\,
200 \,}} \right. \\
& 2\left| \!{\underline {\,
100 \,}} \right. \\
& 2\left| \!{\underline {\,
50 \,}} \right. \\
& 5\left| \!{\underline {\,
25 \,}} \right. \\
& 5\left| \!{\underline {\,
5 \,}} \right. \\
& 1 \\
\end{align}$
On pairing, we get,
$\begin{align}
& =\overline{2\times 2}\times \overline{2\times 2}\times \overline{2\times 2}\times \overline{2\times 2}\times \overline{5\times 5} \\
& =2\times 2\times 2\times 2\times 5 \\
& =16\times 5 \\
& =80 \\
\end{align}$
Hence, we get the square root of 6400 as 80.
Complete step-by-step answer:
It is given in the question that we have to find the square root of the number, 6400. We will use the long division method to find out the square root of 6400. For that, we must first know what square root of a number is. A square root of a number is a value which when multiplied by itself gives the number. The symbol of square root is, $\sqrt{{}}$ which means the positive square root.
Now, we will see the steps for the long division method in order to find the square root.
Step 1: Group the digits in pairs, starting with the unit place. The group number and the remaining digits, if any is called period.
Step 2: Divide with the largest number whose square root is equal to or less than the first period. Take the number as the divisor and also as the quotient.
Step 3: Subtract the product of the divisor and the quotient from the first period to the right of the remainder, this will become the dividend for the next step.
Step 4: The new divisor will be obtained by taking two times the quotient.
Step 5: Repeat steps 2, 3 and 4 till all the periods have been taken. The quotient obtained is the required square root.
Now, by keeping all the steps discussed above in mind, let us find the square root of the number, 6400.
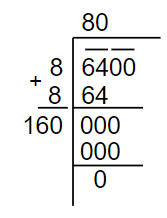
Therefore, the square root of 6400 is 80. It can be represented as $\sqrt{6400}=80$.
Thus, option (b) is the correct answer.
Note: We can also find the square root of 6400 using an alternative method called the prime factorization method, which is as follows.
$\begin{align}
& 2\left| \!{\underline {\,
6400 \,}} \right. \\
& 2\left| \!{\underline {\,
3200 \,}} \right. \\
& 2\left| \!{\underline {\,
1600 \,}} \right. \\
& 2\left| \!{\underline {\,
800 \,}} \right. \\
& 2\left| \!{\underline {\,
400 \,}} \right. \\
& 2\left| \!{\underline {\,
200 \,}} \right. \\
& 2\left| \!{\underline {\,
100 \,}} \right. \\
& 2\left| \!{\underline {\,
50 \,}} \right. \\
& 5\left| \!{\underline {\,
25 \,}} \right. \\
& 5\left| \!{\underline {\,
5 \,}} \right. \\
& 1 \\
\end{align}$
On pairing, we get,
$\begin{align}
& =\overline{2\times 2}\times \overline{2\times 2}\times \overline{2\times 2}\times \overline{2\times 2}\times \overline{5\times 5} \\
& =2\times 2\times 2\times 2\times 5 \\
& =16\times 5 \\
& =80 \\
\end{align}$
Hence, we get the square root of 6400 as 80.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

What is the color of ferrous sulphate crystals? How does this color change after heating? Name the products formed on strongly heating ferrous sulphate crystals. What type of chemical reaction occurs in this type of change.

How do you graph the function fx 4x class 9 maths CBSE

Difference Between Plant Cell and Animal Cell

The largest oil field of India is A Digboi B Bombay class 9 social science CBSE

What is pollution? How many types of pollution? Define it




