Question

How to find the third side of an isosceles triangle? I have the length of the two other legs, which are both $15$ ?

Answer 1

Hint: Problems of this type have non-specific answers, this means that we will be able to find the range between which the answer lies. Using a trigonometric formula of isosceles triangle, we will get the limits between which the length of the third side of an isosceles triangle can exist. So, we can take any value between the limits and conclude it as the answer to the problem.

Complete step by step answer:

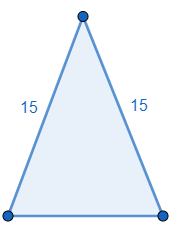
For an isosceles triangle if the given two sides have the same length then for calculating the length of the third side of the triangle, we can use a trigonometric formula for finding the length of the unknown side of the triangle, which is
$l=2\cdot a\cdot sin\left( \dfrac{\theta }{2} \right)$
Here, $l$ is the length of the third side of the triangle, $a$ is the length of the other two sides of the triangle and $\theta $ is the angle between the similar sides of the triangle.
The angle $\theta $ lies between $0$ to $\pi $
We know that $\sin \left( \dfrac{0}{2} \right)=0$ and $\sin \left( \dfrac{\pi }{2} \right)=1$
From the formula we get
$l=2\cdot 15\cdot sin\left( \dfrac{0}{2} \right)$
 $\Rightarrow l=0$ , when $\theta =0$
Also, $l=2\cdot 15\cdot sin\left( \dfrac{\pi }{2} \right)$
$\Rightarrow l=30$ , when $\theta =\pi $
As the angle $\theta $ can take any value between the range $\left( 0,\pi \right)$ the length of the third side of an isosceles triangle can take any value between the range $\left( 0,30 \right)$ .
Therefore, we can conclude that the third side of an isosceles triangle can be of any length between $0$ and $30$ .

Note:
The problem can also be solved by applying the property of triangles. According to a property of triangles the sum of any two sides is greater than the third and the difference between any two sides is less than the third. So, in this case the lower limit for the length of the third side is $0$ and the upper limit for the length of the third side is $30$ . As, $15-15=0$ and $15+15=30$ .