
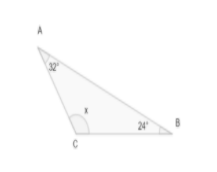
Find the value of x in the following triangle.

Answer
432.1k+ views
Hint: In question it is given that we have a triangle named
Complete step-by-step answer:
ow, from figure we can see that in triangle
Also ,
There is a triangle property of triangles which is known as interior angle sum property. interior angle sum property states that if we have a triangle say
Now, for the figure given in question we have a triangle named
So, using the property of interior angle sum property in triangle
Substituting values of which are given in figure as
On simplifying , we get
Shifting
Subtracting
So, the measure of angle
Note: While solving the numerical based on angles of triangle, or any other polygon, one must know the sum of interior angles or that polygon. In the calculation part, we should be careful that there must not be any calculation error as it may change the answer .
Complete step-by-step answer:
ow, from figure we can see that in triangle
Also ,
There is a triangle property of triangles which is known as interior angle sum property. interior angle sum property states that if we have a triangle say
Now, for the figure given in question we have a triangle named
So, using the property of interior angle sum property in triangle
Substituting values of which are given in figure as
On simplifying , we get
Shifting
Subtracting
So, the measure of angle
Note: While solving the numerical based on angles of triangle, or any other polygon, one must know the sum of interior angles or that polygon. In the calculation part, we should be careful that there must not be any calculation error as it may change the answer .
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

What does R mean in math class 7 maths CBSE

How many crores make 10 million class 7 maths CBSE

Fill in the blanks with appropriate modals a Drivers class 7 english CBSE

The southernmost point of the Indian mainland is known class 7 social studies CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE





