
How do you find the volume of a
Answer
438k+ views
Hint: In order to determine the volume of trapezoid. First, we need to draw a diagram for the trapezoid having the area and length. The formula can be used to calculate the area of a trapezoid,
Complete step by step solution:
In this problem,
We have to find the volume of a
We need to find the area of the base of the trapezium to calculate the volume.
We need to find the area of the trapezoid can be simply defined as the average length of the sides multiplied by the height, using the variables to draw a diagram for representing the area of trapezoid,
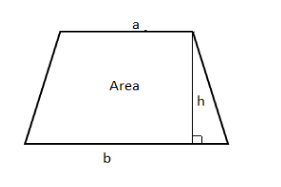
This is the formula for the area of trapezium,
Let
Let
Let
The volume does not exist in two-dimensional statistics. So, you could construct a trapezoidal trapezoid, which is a three-dimensional figure with a trapezoid base. To determine the volume of something, you must first determine the area.
To translate this concept into the three dimension diagram, simply multiply by the trapezoid length:
If the trapezoid length is
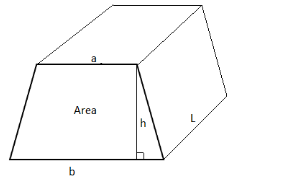
The volume of a
Where,
Finally, we use these methods to find the volume of trapezoid for any given values.
So, the correct answer is “
Note: For example, If the trapezoid length is
We can draw a three dimensional figure with respect to the values given as follows.
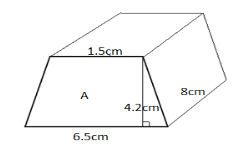
To find the area of trapezoid from the formula, we get
By substitute the values into the formula, we can get
Now, we have to calculate the three dimensional volume of trapezoid is multiplied with length and area of trapezoid, we have
Since, the area is already calculated. So we put that value and the length is given in the figure.
Therefore, the volume of a three dimensional trapezoid is simplified as
Complete step by step solution:
In this problem,
We have to find the volume of a
We need to find the area of the base of the trapezium to calculate the volume.
We need to find the area of the trapezoid can be simply defined as the average length of the sides multiplied by the height, using the variables to draw a diagram for representing the area of trapezoid,

This is the formula for the area of trapezium,
Let
Let
Let
The volume does not exist in two-dimensional statistics. So, you could construct a trapezoidal trapezoid, which is a three-dimensional figure with a trapezoid base. To determine the volume of something, you must first determine the area.
To translate this concept into the three dimension diagram, simply multiply by the trapezoid length:
If the trapezoid length is

The volume of a
Where,
Finally, we use these methods to find the volume of trapezoid for any given values.
So, the correct answer is “
Note: For example, If the trapezoid length is
We can draw a three dimensional figure with respect to the values given as follows.

To find the area of trapezoid from the formula, we get
By substitute the values into the formula, we can get
Now, we have to calculate the three dimensional volume of trapezoid is multiplied with length and area of trapezoid, we have
Since, the area is already calculated. So we put that value and the length is given in the figure.
Therefore, the volume of a three dimensional trapezoid is simplified as
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it





