
Find velocity of piston $A$ in the given situation if angular velocity of wheel of radius $R$ is $m$ (constant), in the clockwise sense. ( $O$ is a fixed point).

A) $\dfrac{{xR\omega \sin \theta }}{{R\cos \theta + x}}$
B) $\dfrac{{{x^2}\omega \sin \theta }}{{R\cos \theta - x}}$
C) $\dfrac{{xR\omega \sin \theta }}{{R\cos \theta - x}}$
D) $\dfrac{{{R^2}\omega \sin \theta }}{{R\cos \theta - x}}$
Answer
233.1k+ views
Hint: Velocity of piston is the change in displacement of piston with respect to time. So, first we will find an expression in terms of all given terms using some geometry. On differentiating the expression, we will find the expression in terms of velocity and angular velocity which will lead us to the expression for velocity.
Complete step by step solution:
In above $\Delta AOB$, $\angle ABO$ is $90^\circ $ (angle between tangent to a circle and it’s radius touching the tangent at circle’s circumference).
$\angle AOB$ is given to us as $\theta $
Let a triangle ABC with standard sides ${\text{a, b, c}}$ and standard angles ${\text{A, B, C}}$ in their standard positions, So, using property of triangle We know that,
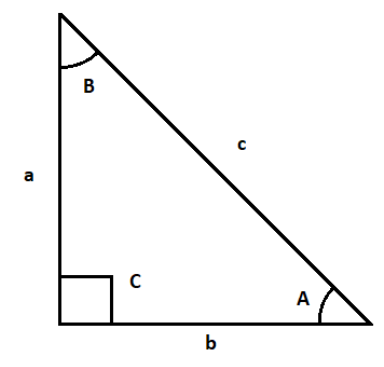
$\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$ and similarly for other angles,
So we can use the above $\cos $ property of triangle in $\Delta AOB$, so we gte,
$\cos \theta = \dfrac{{{R^2} + {x^2} - {L^2}}}{{2Rx}}$
Now we will differentiate this equation with respect to time.
Left side on differentiation:
$\dfrac{{d(\cos \theta )}}{{dt}} = - \sin \theta \dfrac{{d\theta }}{{dt}}$ -----(1)
Right side on differentiation:
$\dfrac{{d\left( {\dfrac{{{R^2} + {x^2} - {L^2}}}{{2Rx}}} \right)}}{{dt}} = \dfrac{{\left( {2Rx} \right)\left( {2x\dfrac{{dx}}{{dt}}} \right) - \left( {{R^2} + {x^2} - {L^2}} \right)\left( {2R\dfrac{{dx}}{{dt}}} \right)}}{{{{\left( {2Rx} \right)}^2}}}$
On simplification we get,
$\dfrac{{\left( {2Rx} \right)\left( {2x\dfrac{{dx}}{{dt}}} \right) - \left( {{R^2} + {x^2} - {L^2}} \right)\left( {2R\dfrac{{dx}}{{dt}}} \right)}}{{{{\left( {2Rx} \right)}^2}}} = \left( {\dfrac{{2R\left( {2{x^2} - {R^2} - {x^2} + {L^2}} \right)}}{{{{\left( {2Rx} \right)}^2}}}} \right)\left( {\dfrac{{dx}}{{dt}}} \right)$
On further simplification, we get,
$ = \dfrac{{{x^2} + {L^2} - {R^2}}}{{2R{x^2}}}\dfrac{{dx}}{{dt}}$ --------(2)
Now equating equations $1$ and $2$, we get,
$ - \sin \theta \dfrac{{d\theta }}{{dt}} = \dfrac{{{x^2} + {L^2} - {R^2}}}{{2R{x^2}}}\dfrac{{dx}}{{dt}}$ ----(3)
Now we know that, $\dfrac{{d\theta }}{{dt}} = \omega $ and $\dfrac{{dx}}{{dt}} = v$
Where $v$ is velocity.
So, on simplifying, we get equation $3$ as,
$ - \sin \theta \times \omega = \dfrac{{{x^2} + {L^2} - {R^2}}}{{2R{x^2}}} \times v$
On simplifying, we get,
$v = - \dfrac{{2R{x^2}\omega \sin \theta }}{{{x^2} + {L^2} - {R^2}}}$
Now, using Pythagoras theorem in $\Delta AOB$, we get,
${L^2} = {x^2} - {R^2}$
Using above equation in expression of velocity we get,
$v = - \dfrac{{2R{x^2}\omega \sin \theta }}{{{x^2} + {x^2} - {R^2} - {R^2}}}$
On simplification we get,
$v = - \dfrac{{R{x^2}\omega \sin \theta }}{{{x^2} - {R^2}}}$
Now, using trigonometric ratio of cos in $\Delta AOB$, we get,
$R = x\cos \theta $
So we get velocity expression on simplification as,
$v = - \dfrac{{R{x^2}\omega \sin \theta }}{{{x^2} - Rx\cos \theta }}$
On further simplification, we get,
$v = \dfrac{{xR\omega \sin \theta }}{{R\cos \theta - x}}$
So the correct answer is option (C).
Note: We were able to find velocity in this way because angular velocity was constant, otherwise, practically, angular velocity of the piston would have increased. This question was all about mathematics and a little bit of physics. You just have to adapt your solution in the form of options using suitable mathematical properties.
Complete step by step solution:
In above $\Delta AOB$, $\angle ABO$ is $90^\circ $ (angle between tangent to a circle and it’s radius touching the tangent at circle’s circumference).
$\angle AOB$ is given to us as $\theta $
Let a triangle ABC with standard sides ${\text{a, b, c}}$ and standard angles ${\text{A, B, C}}$ in their standard positions, So, using property of triangle We know that,

$\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$ and similarly for other angles,
So we can use the above $\cos $ property of triangle in $\Delta AOB$, so we gte,
$\cos \theta = \dfrac{{{R^2} + {x^2} - {L^2}}}{{2Rx}}$
Now we will differentiate this equation with respect to time.
Left side on differentiation:
$\dfrac{{d(\cos \theta )}}{{dt}} = - \sin \theta \dfrac{{d\theta }}{{dt}}$ -----(1)
Right side on differentiation:
$\dfrac{{d\left( {\dfrac{{{R^2} + {x^2} - {L^2}}}{{2Rx}}} \right)}}{{dt}} = \dfrac{{\left( {2Rx} \right)\left( {2x\dfrac{{dx}}{{dt}}} \right) - \left( {{R^2} + {x^2} - {L^2}} \right)\left( {2R\dfrac{{dx}}{{dt}}} \right)}}{{{{\left( {2Rx} \right)}^2}}}$
On simplification we get,
$\dfrac{{\left( {2Rx} \right)\left( {2x\dfrac{{dx}}{{dt}}} \right) - \left( {{R^2} + {x^2} - {L^2}} \right)\left( {2R\dfrac{{dx}}{{dt}}} \right)}}{{{{\left( {2Rx} \right)}^2}}} = \left( {\dfrac{{2R\left( {2{x^2} - {R^2} - {x^2} + {L^2}} \right)}}{{{{\left( {2Rx} \right)}^2}}}} \right)\left( {\dfrac{{dx}}{{dt}}} \right)$
On further simplification, we get,
$ = \dfrac{{{x^2} + {L^2} - {R^2}}}{{2R{x^2}}}\dfrac{{dx}}{{dt}}$ --------(2)
Now equating equations $1$ and $2$, we get,
$ - \sin \theta \dfrac{{d\theta }}{{dt}} = \dfrac{{{x^2} + {L^2} - {R^2}}}{{2R{x^2}}}\dfrac{{dx}}{{dt}}$ ----(3)
Now we know that, $\dfrac{{d\theta }}{{dt}} = \omega $ and $\dfrac{{dx}}{{dt}} = v$
Where $v$ is velocity.
So, on simplifying, we get equation $3$ as,
$ - \sin \theta \times \omega = \dfrac{{{x^2} + {L^2} - {R^2}}}{{2R{x^2}}} \times v$
On simplifying, we get,
$v = - \dfrac{{2R{x^2}\omega \sin \theta }}{{{x^2} + {L^2} - {R^2}}}$
Now, using Pythagoras theorem in $\Delta AOB$, we get,
${L^2} = {x^2} - {R^2}$
Using above equation in expression of velocity we get,
$v = - \dfrac{{2R{x^2}\omega \sin \theta }}{{{x^2} + {x^2} - {R^2} - {R^2}}}$
On simplification we get,
$v = - \dfrac{{R{x^2}\omega \sin \theta }}{{{x^2} - {R^2}}}$
Now, using trigonometric ratio of cos in $\Delta AOB$, we get,
$R = x\cos \theta $
So we get velocity expression on simplification as,
$v = - \dfrac{{R{x^2}\omega \sin \theta }}{{{x^2} - Rx\cos \theta }}$
On further simplification, we get,
$v = \dfrac{{xR\omega \sin \theta }}{{R\cos \theta - x}}$
So the correct answer is option (C).
Note: We were able to find velocity in this way because angular velocity was constant, otherwise, practically, angular velocity of the piston would have increased. This question was all about mathematics and a little bit of physics. You just have to adapt your solution in the form of options using suitable mathematical properties.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




