Question

How do you find vertical asymptote of tangent function ?

Answer 1

Hint: In the given question, we are required to find out the vertical asymptotes of the tangent function. Asymptote is a straight line that continually approaches a given curve but does not meet it at any finite distance. So to find vertical asymptotes for tangent function, we have to calculate the derivative of the function and see the nature of the curve at different points. Then, we equate the derivative of the function to infinity so as to find the points where the vertical asymptotes for the tangent function exists.

Complete step by step solution:
To solve the given question and find the vertical asymptote of tangent function, we first find out the derivative of the function.
So, $ f\left( x \right) = \tan \left( x \right) $
Hence, $ f'\left( x \right) = {\sec ^2}\left( x \right) $
Now, equating the derivative to infinity since the slope of the function has to be infinity so as to have a vertical asymptote.
So, for $ f'\left( x \right) = {\sec ^2}x = \dfrac{1}{{{{\cos }^2}\left( x \right)}} $ to be infinity, the denominator must be zero.
Hence, we get, $ {\cos ^2}\left( x \right) = 0 $
 $ \Rightarrow \cos \left( x \right) = 0 $
 $ \Rightarrow x = \left( {\dfrac{{n\pi }}{2}} \right) $ where n is any integer.
So, the tangent function has a vertical asymptote for every integral multiple of $ \left( {\dfrac{\pi }{2}} \right) $ .

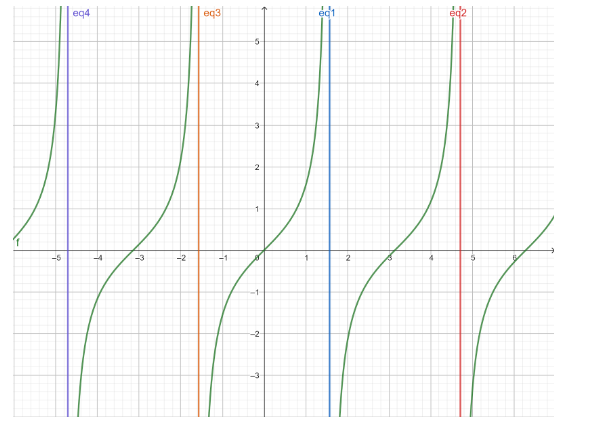
Note: One should have thorough knowledge of differentiation and applications of derivatives in order to solve such questions. We should also know the definition of an asymptote. Algebraic rules like transposition must also be practiced as they are used often in mathematical equations.