Question

Fluid is flowing with velocity 4m/s in a cylinder of diameter 8 cm. It is connected to a pipe with its end tip of diameter 2 cm. Calculate the velocity of the fluid at this free end.
A. 4m/s
B. 8m/s
C. 32m/s
D. 64m/s

Answer 1

Hint: When fluid is flowing through a pipe, the volume has to be conserved per unit time. This means the rate of volume entering must be equal to the rate of exiting. This result is called the equation of continuity which is a very important result of a principle known as Bernoulli’s principle.
Formula used: $\dfrac{dV}{dt} = A_1 v_1 = A_2 v_2$

Complete step-by-step solution

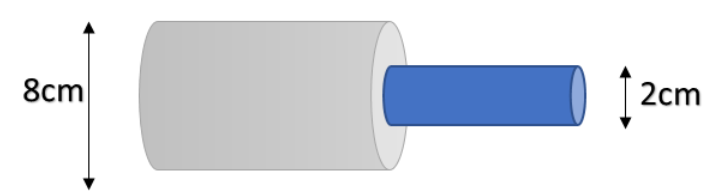
 As shown in the above diagram, we have the fluid getting enter in the thicker tube and getting exit from the narrow tube. Now, according to the equation of continuity, $A_1v_1 = A_2v_2$
Given: $d_1 = 8cm \implies A_1 = \dfrac{\pi}{4}(8)^2$
And $d_2 = 2cm \implies A_2 = \dfrac{\pi}{4}(2)^2$
Also $v_1 = 4 m/s$
Hence putting these values in equation $A_1v_1 = A_2v_2$, we get;
$\dfrac{\pi}{4} \times 8^2 \times 4 = \dfrac{\pi}{4} \times 2^2 \times v_2$
$\implies v_2 = 8^2 = 64 m/s$.
Thus, option D. is correct.
Additional information: The term$\dfrac{dV}{dt}$represents the rate of flow of fluid. It means the total volume of fluid flow per unit time. Hence we can calculate this term if we know the variation of volume with time. Equation of continuity plays a very important role in fluid mechanics. Even in the case of varying cross-sectional areas, we could get the point to point relation between area and velocity of the fluid molecule at that point. The measuring area of cross-section is an easier task, compared to the velocity. Hence using this equation, we can analyze the complex situation of the velocity behavior of the fluid.

Note: There are certain assumptions that Bernoulli assumed while deriving this theorem. This includes that fluid must be incompressible and the flow of fluid must be laminar flow. This type of fluid is called an ideal fluid. But practically, it’s very difficult for fluid to behave like an ideal fluid.