Question

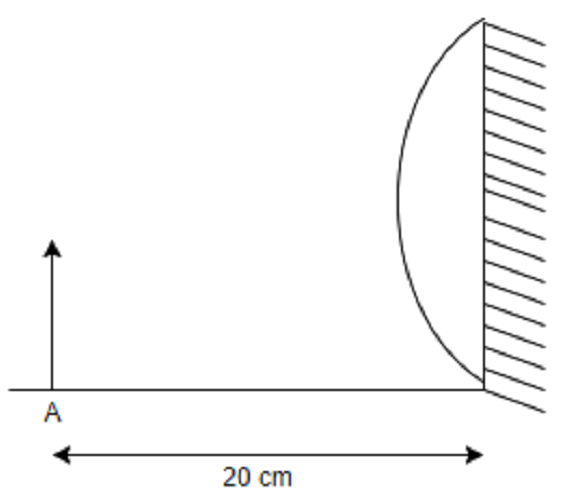
Focal length of the plano-convex lens is 15 cm. A small object is placed at \[A\] as shown in the figure. The plane surface is silvered. The image will form at?

A. 60 cm to the left of the lens
B. 12 cm to the left of the lens
C. 60 cm to the right of the lens
D. 30 cm to the left of the lens

Answer 1

Hint: Here we will proceed by using the concept of mirror formula. By using the mirror formula and plano-convex lens formula, we will find out the focal length.
Formula Used:
1. For the plane surface mirror, focal length formula is given by \[\dfrac{1}{v} + \dfrac{1}{u} =
\dfrac{1}{F}\]
Where, \[u\] is the distance of object
\[v\] is the distance of image
\[F\] is the focal length of the mirror.
2. For the plano-convex lens, focal length formula is given by \[\dfrac{1}{F} = \dfrac{2}{f} +
\dfrac{1}{{{f_m}}}\]
Where, \[F\] is the focal length of the mirror
\[f\] is the focal length of the plano-convex lens
\[{f_m}\] is the focal length of the plane surface

Complete step-by-step solution:
Given that a ray from point O at first gets refracted from the curved surface of focal length, \[f = 15cm\] and then reflects from the plane mirror. Hence the plano-convex lens will become a curved mirror of focal length \[F\]. So, we have
\[\dfrac{1}{F} = \dfrac{1}{{{f_m}}} - \dfrac{2}{f}{\text{ }}\left[{\because {\text{ focal length of plano convex lens is negative}}} \right]\]
Where \[{f_m}\] is the local length of mirror used which equals to infinity \[\left( \infty \right)\]
\[ \Rightarrow \dfrac{1}{F} = \dfrac{1}{\infty } - \dfrac{2}{{15}} \\ \]
\[ \Rightarrow \dfrac{1}{F} = 0 - \dfrac{2}{{15}} \\ \]
\[\therefore F = \dfrac{{ - 15}}{2}{\text{ cm}} \]
From the given figure, we have \[u = - 20\,{\text{cm}}\]
By using formula of focal length for a plane mirror i.e., \[\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{F}\]
We get
\[\Rightarrow\dfrac{1}{v}-\dfrac{1}{20} = -\dfrac{2}{{15}}\left[ {\because F = \dfrac{{ - 15}}{2}} \right] \\
\Rightarrow \dfrac{1}{v} = \dfrac{1}{{20}} - \dfrac{2}{{15}} \\
\Rightarrow \dfrac{1}{v} = - \dfrac{1}{{12}} \\
\therefore v = - 12{\text{ cm}} \]
The negative sign indicates that the image is 12 cm in front of the mirror.
Thus, the final image will form at 12 cm to the left of the lens. Hence, the correct option is B. 12 cm to the left of the lens.

Note: Whenever we come up with this type of question, one must know the distance between the center of a lens or curved mirror and its focus. Then we will apply the mirror formula and put the values in place of the formula. After solving that we will get our answer.