Question

Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes. \[\]

Answer 1

Hint: We assume the radius of circle in the second quadrant and touching the coordinate axes as $a$. We find the coordinates of centre of the circle in terms of $a$ and write the equation of the circle in centre $\left( {{x}_{1}},{{y}_{1}} \right)$ radius form as ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{a}^{2}}$. We differentiate the equation with respect to $x$ and find the values of $a$ in terms of variables and differentials. We put $a$ in the equation of the circle and simplify to obtain the required equation. \[\]

Complete step by step answer:
We know that differential equations are an equation that involves functions, variables and their derivatives. A family of curves is a set of curves, each of which is given by a function or parameterization in which one or more of the parameters is variable. The parametric equation of the family of circles with parameter $t$ is given by
\[x=r\cos t,y=r\sin t\]
We know that the equation of the circle with centre $\left( {{x}_{1}},{{y}_{1}} \right)$ and radius $r$ is given by,
\[{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}\]
Let $C$ be the circle with radius $a$ which touches the $x-$axis at the point $A\left( -a,0 \right)$and $y-$axis at the point $B\left( 0,a \right)$ and is present in the second quadrant. The co-ordinates of the centre G of the circle is$G\left( -a,a \right)$.
 

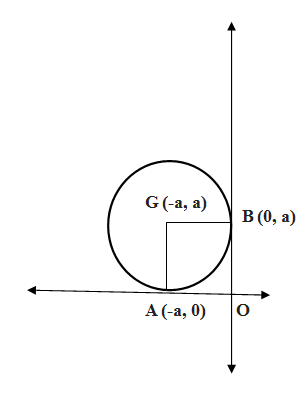
The equation of family of circles in centre-radius from is given by
\[\begin{align}
  & {{\left( x-\left( -a \right) \right)}^{2}}+{{\left( y-a \right)}^{2}}={{a}^{2}} \\
 & \Rightarrow {{\left( x+a \right)}^{2}}+{{\left( y-a \right)}^{2}}={{a}^{2}}....\left( 1 \right) \\
\end{align}\]

We have to eliminate $a$ from the above equation. Let us differentiate the above equation with respect to $x$ by chain rule and have,
\[\begin{align}
  & \Rightarrow \dfrac{d}{dx}\left[ {{\left( x+a \right)}^{2}}+{{\left( y-a \right)}^{2}} \right]=\dfrac{d}{dx}{{a}^{2}} \\
 & \Rightarrow 2\left( x+a \right)\dfrac{d}{dx}\left( x+a \right)+2\left( y-a \right)\dfrac{d}{dx}\left( y-a \right)=0 \\
 & \Rightarrow \left( x+a \right)\cdot 1+\left( y-a \right){{y}^{'}}=0 \\
\end{align}\]
Here we have denoted the differential${{y}^{'}}=\dfrac{dy}{dx}$. Let us find the value of $a$ from the above equation
\[\begin{align}
  & \Rightarrow \left( x+a \right)\cdot 1+\left( y-a \right){{y}^{'}}=0 \\
 & \Rightarrow x+y{{y}^{'}}=a\left( {{y}^{'}}-1 \right) \\
 & \Rightarrow a=\dfrac{x+y{{y}^{'}}}{{{y}^{'}}-1} \\
\end{align}\]
We put the expression for $a$ in equation (1) and have,

\[\begin{align}
  & {{\left( x+\dfrac{x+y{{y}^{'}}}{{{y}^{'}}-1} \right)}^{2}}+{{\left( y-\dfrac{x+y{{y}^{'}}}{{{y}^{'}}-1} \right)}^{2}}={{\left( \dfrac{x+y{{y}^{'}}}{{{y}^{'}}-1} \right)}^{2}} \\
 & \Rightarrow {{\left( \dfrac{x{{y}^{'}}-x+x+y{{y}^{'}}}{{{y}^{'}}-1} \right)}^{2}}+{{\left( \dfrac{y{{y}^{'}}-y-x-y{{y}^{'}}}{{{y}^{'}}-1} \right)}^{2}}={{\left( \dfrac{x+y{{y}^{'}}}{{{y}^{'}}-1} \right)}^{2}} \\
 & \Rightarrow {{\left( \dfrac{x{{y}^{'}}+y{{y}^{'}}}{{{y}^{'}}-1} \right)}^{2}}+{{\left( \dfrac{-y-x-}{{{y}^{'}}-1} \right)}^{2}}={{\left( \dfrac{x+y{{y}^{'}}}{{{y}^{'}}-1} \right)}^{2}} \\
 & \Rightarrow \dfrac{{{\left( \left( x+y \right){{y}^{'}} \right)}^{2}}}{{{\left( {{y}^{'}}-1 \right)}^{2}}}+\dfrac{{{\left( x+y \right)}^{2}}}{{{\left( {{y}^{'}}-1 \right)}^{2}}}=\dfrac{{{\left( x+y{{y}^{'}} \right)}^{2}}}{{{\left( {{y}^{'}}-1 \right)}^{2}}} \\
\end{align}\]
Let us multiply ${{\left( {{y}^{'}}-1 \right)}^{2}}$ in all the terms of the equation and have
\[\begin{align}
  & \dfrac{{{\left( \left( x+y \right){{y}^{'}} \right)}^{2}}}{{{\left( {{y}^{'}}-1 \right)}^{2}}}+\dfrac{{{\left( x+y \right)}^{2}}}{{{\left( {{y}^{'}}-1 \right)}^{2}}}=\dfrac{{{\left( x+y{{y}^{'}} \right)}^{2}}}{{{\left( {{y}^{'}}-1 \right)}^{2}}} \\
 & \Rightarrow {{\left( x+y \right)}^{2}}{{\left( {{y}^{'}} \right)}^{2}}+{{\left( x+y \right)}^{2}}={{\left( x+y{{y}^{'}} \right)}^{2}} \\
 & \Rightarrow {{\left( x+y \right)}^{2}}\left[ {{\left( {{y}^{'}} \right)}^{2}}+1 \right]={{\left( x+y{{y}^{'}} \right)}^{2}} \\
\end{align}\]

The above equation is the required differential equation of family circles which contains variables $x,y$ and the differential ${{y}^{'}}=\dfrac{dy}{dx}$.\[\]

Note: The highest derivative in the differentiation equation is called order and the obtained differential equation is of first order. The obtained differential equation is also ordinary because we have treated $y$ as the dependent and $x$ as the independent variable. If we would have treated both $x,y$ as independent , we would have obtained a pair of partial differential equations.