Question

Four resistance$10\,ohm,10\,ohm,10\,ohm$ and $15\,ohm$ form a Wheatstone’s network. What shunt is required across $15ohm$ resistor to balance the bridge?
A. $10\,ohm$
B. $15\,ohm$
C. $20\,ohm$
D. $30\,ohm$

Answer 1

Hint:Learn the working principle of Wheatstone’s bridge. The principle states the ratio of the resistances are equal and no current flows through the circuit. This works on the principle of null deflection. Applying the resistance ratio we can get the shunt resistance value.

Formula Used:
$\left( {\dfrac{{{R_1}}}{{{R_2}}}} \right) = \left( {\dfrac{{{R_3}}}{{{R_4}}}} \right)$
Where,
${R_1},{R_2},{R_3},{R_4}$ are resistances of the Wheatstone’s bridge

Complete step by step answer:
According to the question we know that there are four resistance connected as a wheatstone network. Where, ${R_1} = {R_2} = {R_3} = 10\,ohm$ and ${R_4} = 15\,ohm$.Applying the Wheatstone bridge Principe all these four resistance ratios are equal respectively.

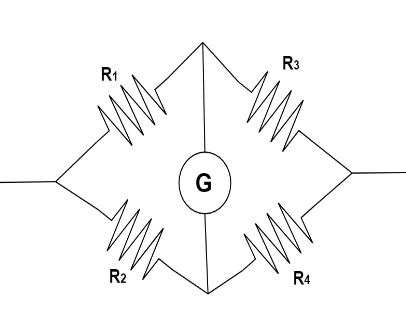
We know that,
$\left( {\dfrac{{{R_1}}}{{{R_2}}}} \right) = \left( {\dfrac{{{R_3}}}{{{R_4}}}} \right) \ldots \ldots \left( 1 \right)$
And, if this condition is satisfied then this is a Wheatstone bridge network.By putting the respective value in the equation $\left( 1 \right)$ we get,
$\dfrac{{10\,ohm}}{{10\,ohm}} = \dfrac{{10\,ohm}}{{15\,ohm}}$
To equate the above ratio we have to make that $15\,ohm$ to $10\,ohm$.Equating the above equation is quite necessary because the galvanometer connected between them will give zero current as an output so as to satisfy the Wheatstone bridge principle.As $15\,ohm$ greater than $10\,ohm$ of resistance we have to decrease the $15\,ohm$ resistance to get an exact ratio, hence the shunt resistor must be connected parallel to the of resistor because a parallel resistance only decreases the equivalent resistance while series connection give a greater value.

So connect a shunt resistance ${R_S}$ parallely across the $15\,ohm$ resistor which decreases the overall value of the $15\,ohm$ resistor.Hence after connecting the shunt resistance across the $15\,ohm$ we get,
$\dfrac{1}{{10}} = \dfrac{1}{{15}} + \dfrac{1}{{{R_s}}}$
$ \Rightarrow \dfrac{1}{{10}} = \dfrac{{{R_S} + 15}}{{15{R_s}}}$
Taking reciprocal on both sides,
$ \Rightarrow 10 = \dfrac{{15{R_S}}}{{{R_S} + 15}}$
$ \Rightarrow 10\left( {{R_S} + 15} \right) = 15{R_S}$
$ \Rightarrow 10{R_S} + 150 = 15{R_S}$
Shifting the terms in the equation, we get,
$ \Rightarrow 150 = 15{R_S} - 10{R_S}$
$ \Rightarrow 150 = 5{R_S}$
$ \therefore {R_S} = 30\,ohm$
Hence $30\,ohm$ shunt is required across $15\,ohm$ resistor to balance the bridge.

Therefore the correct option is $\left( D \right)$.

Note:The shunt resistance must be connected in parallel with the $15\,ohm$ resistance because if we connect the shunt resistance in series with the $15\,ohm$ resistance then we will not exact the exact equal ratio according to the Wheatstone bridge principle.