Question

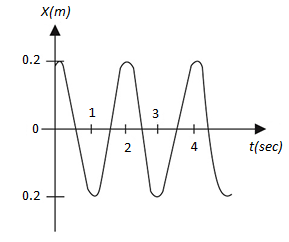
From the displacement time graph of an oscillating particle, find the maximum velocity of the particle.

A. \[2\,m{s^{ - 1}}\]
B. \[\pi \,m{s^{ - 1}}\]
C. \[0.2\pi \,m{s^{ - 1}}\]
D. \[\dfrac{\pi }{2}\,m{s^{ - 1}}\]

Answer 1

Hint: From the given displacement-time graph determine the period of oscillation. Amplitude of the oscillation is the distance between the mean position and extreme position. Use the formula for maximum velocity of the particle performing S.H.M.

Formula used:
The maximum velocity of the particle performing S.H.M is given by,
\[{v_{\max }} = \omega A\]
Here, \[\omega \] is the angular frequency and A is the amplitude of the oscillations.
The angular frequency of the particle is,
\[\omega = \dfrac{{2\pi }}{T}\]
Here, \[T\] is the period of the oscillation.

Complete step by step answer:
We know that the maximum velocity of the particle performing S.H.M is given by,
\[{v_{\max }} = \omega A\] …… (1)

Here, \[\omega \] is the angular frequency and A is the amplitude of the oscillations.

Therefore, from the above equation we need to determine the amplitude and angular frequency of the oscillations.
We know that the amplitude of the oscillations is the maximum vibration of the particle from its mean position. From the above equation, we can observe that the amplitude of the oscillation is 0.2 m.

We have the relation between angular frequency and period of the particle performing S.H.M as,
\[\omega = \dfrac{{2\pi }}{T}\]

Here, \[T\] is the period of the oscillation.

The period of oscillation is the time taken by the particle to complete one oscillation. One oscillation is the one complete wavelength of the particle. From the above equation, the time required to complete one oscillation is 2 seconds.

Therefore, the angular frequency of the oscillations is,
\[\omega = \dfrac{{2\pi }}{2}\]
\[ \Rightarrow \omega = \pi \,rad/s\]

We substitute \[\pi \,rad/s\] for \[\omega \] and 0.2 m for T in equation (1).
\[{v_{\max }} = \left( \pi \right)\left( {0.2\,} \right)\]
\[ \Rightarrow {v_{\max }} = 0.2\pi \,m{s^{ - 1}}\]
Therefore, the maximum velocity of the particle is \[0.2\pi \,m{s^{ - 1}}\].

So, the correct answer is option (C).

Note:
While determining the wavelength of the particle in a displacement-time graph, students should measure the distance between the adjacent crests or the adjacent troughs if the particle does not start from the mean position. Students should always remember that the amplitude is the distance from the mean position to the extreme position and not the distance between the two extremes.