Question

Give one example of damped vibration.

Answer 1

Hint: If we swing a pendulum, having a certain length of the string, we will see at first oscillation it reaches its maximum height and after that gradually height decreases with the number of oscillations. This is due to opposing forces like air drag. The time comes when the pendulum finally stops. This is the damping of vibration or we can say that it is losing energy. We will see in brief why this happens.

Complete step by step answer:
To give one example of damped oscillation let us understand the damped oscillation first:
Damped Oscillation:
In an ideal condition energy and amplitude of SHM (simple harmonic motion) remains constant. Mathematically, displacement of SHM is given by

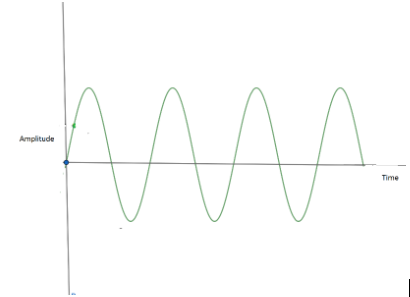
$x=a\sin \left( \omega t+\phi \right)$
Where,
\[x=\]displacement of particle executing SHM
\[a=\] amplitude
\[\phi =\] phase difference
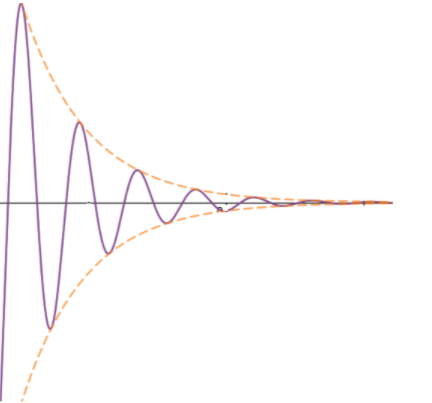
In practical situations a resistance act on the particle which is known as damping force. Damping force is directly proportional to velocity of particle, but its direction is always opposite to velocity due to which amplitude and energy of SHM decrease simultaneously. This is known as damped oscillation of damped vibration.
Let the damping force acting on the particle is F and the velocity of particle be v, then:
\[\begin{align}
  & F\propto -v \\
 & F=-bv \\
\end{align}\]
Here negative sign indicates damping and b is the damping constant.
As a result of this force we obtain this type of graph

Examples of damped vibrations are: Clock pendulum, Vibrating spring, LRC circuits etc.

Note: If oscillations are damping then to revive damped oscillation we have to give continuous energy to maintain its amplitude with a period of time, and the oscillation obtained is called Forced Oscillation.
Therefore it is to be clear in mind what is damped oscillation and what is Forced oscillation.