Question

Give the condition for constructive and destructive interference in terms of phase difference and path difference.

Answer 1

Hint: During the phenomenon of interference, the disturbance that the two waves have formed their mean positions add up to form a new wave that has the same disturbance from the mean position as the sum of the two initial disturbances. We will give the conditions such that the final wave has twice the disturbance for constructive interference and no disturbance for destructive interference.

Complete step by step answer:
Interference is the phenomenon in which two waves superpose to form a new wave which may have an amplitude greater than, lower than, or the same amplitude as the original waves. Interference results from the interaction of waves that come from the same source or they have the same or nearly the same frequency.
Constructive interference will happen when the peaks of both the waves are at the same place and troughs of both the waves are at the same place that will happen only when the path difference is zero or some even multiple of $\pi$. There must be complete waves between them, so the path difference will need to be an integral multiple of the wavelength of the wave.

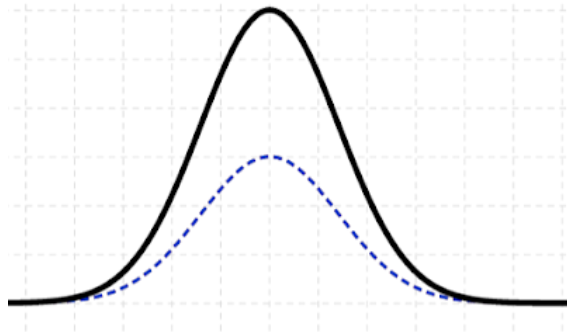
So, for constructive interference we get
Phase difference = 2nπ (n=0,1,2,3…….)
Path difference = nλ(n=0,1,2,3…….)
Destructive interference will happen when the peaks of one the waves are at the same place as the troughs of the other wave. That will happen only when the path difference is some odd multiple of $\pi$. There must be half a wave between them or one half wave in addition to any number of complete waves so, the path difference will need to be the difference of an integral multiple of the wavelength of the wave and half of the wavelength.

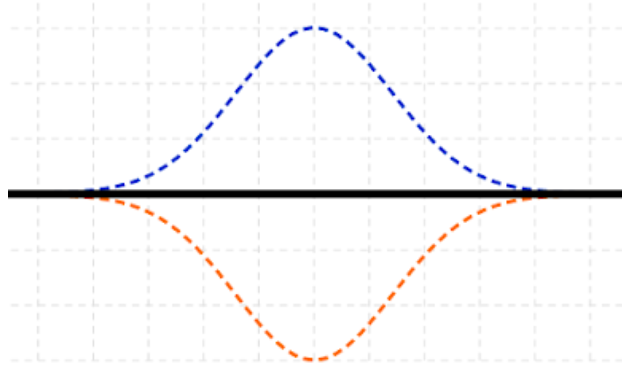
So, for Destructive interference we get
Phase difference = (2n+1)π (n=0,1,2,3…….)
Path difference = (2n+1)λ/2(n=0,1,2,3…….)

Note: A better interference pattern is observed when the frequencies of the two constituent waves are closer to each other. Best pattern is obtained when their frequencies are exactly the same. We will be getting constructive interference only when both the troughs are in the same place because the intensity is proportional to the square of the disturbance so the intensity will be maximum here.