
How do I graph the quadratic equation \[y={{\left( x-1 \right)}^{2}}\] by plotting points?
Answer
449.7k+ views
Hint: The given type of problem is very simple and easy to solve. This problem is of topic “Coordinate Geometry” and of sub-topic “Parabola”. For solving these types of problems we need to first keep in mind the different general forms of parabolas possible in coordinate geometry. There are four general types of parabola and for each of them, the corresponding vertex and foci are as follows,
Now, starting off with the solution of our given problem, to plot the equation, we first need to find two things to our problem, they are,
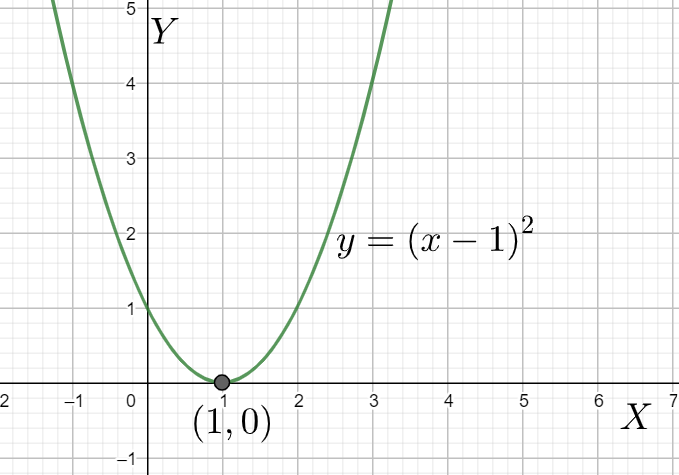
\[1.\] Finding out the vertex of the parabola, and plotting that point on the graph paper.
\[2.\] Finding out the roots of the equation and plotting the point on the graph paper.
Now, if we take a closer look at the problem, we see that the equation has double roots, i.e. both the roots of the equation are same and equal to \[1\] . We find the roots of the equation by making \[y=0\] and finding out the corresponding value of \[x\] .
After that we find the value of the vertex of the parabola. We should remember that the parabola would be symmetric about a vertical line passing through the vertex. Comparing the given equation of the parabola with the general equation of the parabola \[{{x}^{2}}=4by\], we get the vertex of the parabola to be \[\left( 1,0 \right)\] . Knowing all these information, we thus plot the given equation on the graph paper as,
Note:
We can also solve the above problem, using another alternate method, i.e. by finding the critical points using the first derivative of the function. We then find the second derivative to know the nature of the curve, and try to find any lines of symmetry as well. We must always remember all the general forms of the parabolas, because they are very essential to compare with the given parabolic equation and find out the necessary details of the problem.
| Equation | Vertex | Foci |
| \[{{y}^{2}}=4ax\] | \[\left( 0,0 \right)\] | \[\left( a,0 \right)\] |
| \[{{y}^{2}}=-4ax\] | \[\left( 0,0 \right)\] | \[\left( -a,0 \right)\] |
| \[{{x}^{2}}=4by\] | \[\left( 0,0 \right)\] | \[\left( 0,b \right)\] |
| \[{{x}^{2}}=-4by\] | \[\left( 0,0 \right)\] | \[\left( 0,-b \right)\] |
Now, starting off with the solution of our given problem, to plot the equation, we first need to find two things to our problem, they are,
\[1.\] Finding out the vertex of the parabola, and plotting that point on the graph paper.
\[2.\] Finding out the roots of the equation and plotting the point on the graph paper.
Now, if we take a closer look at the problem, we see that the equation has double roots, i.e. both the roots of the equation are same and equal to \[1\] . We find the roots of the equation by making \[y=0\] and finding out the corresponding value of \[x\] .
After that we find the value of the vertex of the parabola. We should remember that the parabola would be symmetric about a vertical line passing through the vertex. Comparing the given equation of the parabola with the general equation of the parabola \[{{x}^{2}}=4by\], we get the vertex of the parabola to be \[\left( 1,0 \right)\] . Knowing all these information, we thus plot the given equation on the graph paper as,

Note:
We can also solve the above problem, using another alternate method, i.e. by finding the critical points using the first derivative of the function. We then find the second derivative to know the nature of the curve, and try to find any lines of symmetry as well. We must always remember all the general forms of the parabolas, because they are very essential to compare with the given parabolic equation and find out the necessary details of the problem.
Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

What is a transformer Explain the principle construction class 12 physics CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




