Question

Graph $y = \sqrt {x - 1} $ and how does it compare it to the parent function?

Answer 1

Hint: This problem deals with finding the graph of the given function. After finding the graph of the function, we have to compare the graph with the graph of the parent function of the given function. In mathematics, a parent function is the simplest function of a family of function that preserves the definition of the entire family.

Complete step by step answer:
Let $y = f(x)$
So here the parent function is $f(x) = \sqrt x $, so the child function is obtained by computing $f\left( {x - 1} \right)$ instead of $f(x)$. The transformation belongs to the family of the horizontal translations, which happens every time you change from $f(x)$ to $f(x + k)$.
In particular, we can translate $k$ units to the left if $k > 0$, or $k$ units to the right if $k < 0$.
In this case the value of $k$ is equal to -1, that is $k = - 1$, so this function is drawn by shifting the parent function one unit to the right as shown below:
The red marked curve is the graph of $f(x) = \sqrt x $, whereas the green marked curve is the graph of $f(x) = \sqrt {x - 1} $.

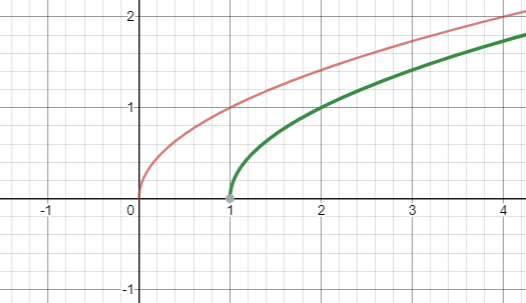
We can observe from both the graphs that both the graphs are identical, but for the child function there is the right translation of 1 unit.

Note: Please note that the parent function is the simplest function that still satisfies the definition of a certain type of function. For example, when we think of the linear functions which make up a family of functions, the parent function would be $y = x$. The child function is used to add the element as a child element to the parent element.