Question

What is the greatest common factor of \[16\] and \[20\]?

Answer 1

Hint: Greatest common factor also called GCF. The greatest common factor of two or more numbers is the largest possible number which divides the given numbers without any remainder.
We can find GCF by any of the following methods
1. Prime factorization method.
2. Listing the common factors method.
3. Long division method.

Complete step-by-step answer:
From the question it is clear that we have to find the greatest common factor of \[16\] and \[20\].
From the basic concepts of mathematics, we know that the greatest common factor of two or more numbers is the largest possible number which divides the given numbers without any remainder.
Now let us try to find the greatest common factor of \[16\] and \[20\] by a prime factorization method.
In the prime factorization method, first we have to write the given numbers as the product of prime numbers.
Now, Let us try to write \[16\] and \[20\] as a product of its prime numbers.

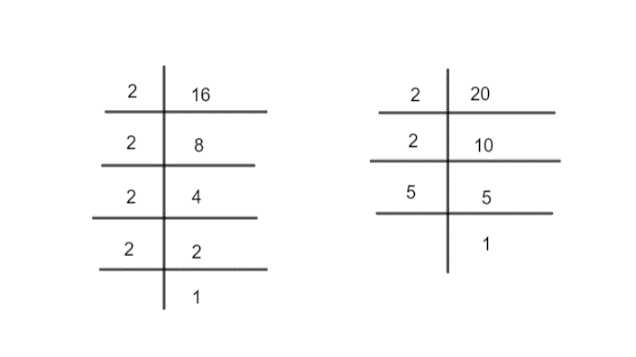
Prime factorization of \[16\]
\[\Rightarrow 16=2\times 2\times 2\times 2\times 1\]
Prime factorization of \[20\]
\[\Rightarrow 20=2\times 2\times 5\times 1\]
From the prime factorization of \[16\] and \[20\], we can see common factors \[2,2\].
The greatest common factor is the product of factors that are common to each of the given numbers.
so GCF is \[2\times 2=4\]
Now we can conclude that the greatest common factor of \[16\] and \[20\] is \[4\].

Note: While doing factorization we have to take only factors that are prime numbers. to make this method simple try to factorize the given numbers in the pictorial manner as shown. Students should be careful while doing calculations because it may lead to big errors in the answer.