Question

How do you graph $ y = 3\sin 4x $ ?

Answer 1

Hint: In this question, we are given a sine function and we have to plot its graph. For plotting the graph of any function, we have to first convert the function to the standard form, and then we compare the given function with its standard equation. The standard form of the sine equation is $ y = A\sin (Bx + C) + D $ . On comparing the two equations, we can find out how the graph should be plotted.

Complete step-by-step answer:
We are given that $ y = 3\sin 4x $ and we know that the standard form is $ y = A\sin (Bx + C) + D $ ,
Comparing these two equations, we get –
 $ A = 3,\,B = 4,\,C = 0\,and\,D = 0 $
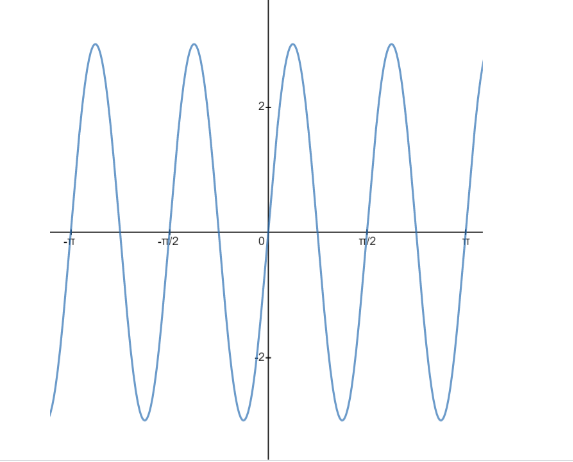
Amplitude of the given sine function is 3, so the given sine function has peak values at 3 and -3, that is, it oscillates between 3 and -3 and the given sine function completes four oscillations between 0 and $ 2\pi $ , but for plotting the graph, we have to find out the period of the function. Period of a sine function is –
 $
  p = \dfrac{{2\pi }}{B} \\
   \Rightarrow p = \dfrac{{2\pi }}{4} = \dfrac{\pi }{2} \;
  $
That is the given function repeats the oscillation after every $ \dfrac{\pi }{2} $ radians, it completes 1 oscillation in the interval 0 to $ \dfrac{\pi }{2} $ .
Now, we know all the quantities that are required for plotting the graph of the given function, so the graph of $ y = 3\sin 4x $ is plotted as follows –

Note: We know that the general form of the sine function is $ y = A\sin (Bx + C) + D $ where
A tells us the value of the peaks of the function, that is, A is the amplitude.
B tells us the number of oscillations a function does in a fixed interval, that is, B is the frequency.
C and D denote the horizontal and vertical shift of a function respectively. There is no horizontal or vertical shift in the graph of this function as the value of C and D is zero for the given function.