
How do you graph \[y = \sqrt {x - 1} - 3\]?
Answer
476.4k+ views
Hint: To graph \[y = \sqrt {x - 1} - 3\], we know that the parent function of the functions of the form \[f(x) = \sqrt {x - a} + b\] is \[f(x) = \sqrt x \]. So, we will start with the graph of \[y = \sqrt x \]. Then change \[x\] to \[x - 1\] to obtain \[y = \sqrt {x - 1} \]. Then we will translate the graph \[3\] units down to obtain the graph of \[y = \sqrt {x - 1} - 3\].
Complete step by step answer:
We have to graph \[y = \sqrt {x - 1} - 3\]. We can also write this as \[y - \left( { - 3} \right) = \sqrt {x - 1} \].
The parent function of the functions of the form \[f(x) = \sqrt {x - a} + b\] is \[f(x) = \sqrt x \].
Here, the domain of \[f(x) = \sqrt x \] is \[x \geqslant 0\] and the range is \[y \geqslant 0\].
We can graph \[y = \sqrt x \] as follows:
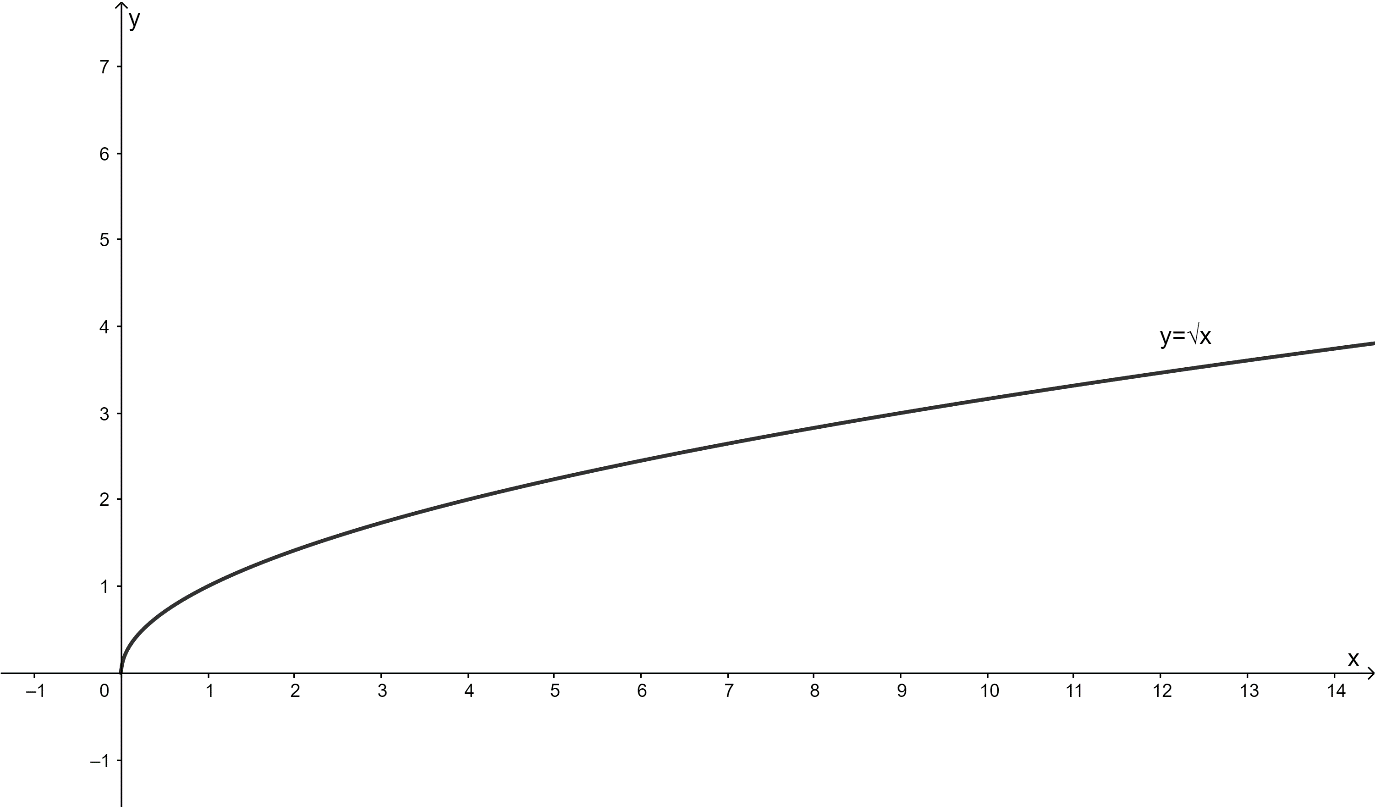
Now we will move the graph of \[y = \sqrt x \] by \[1\] unit to the right to obtain the graph of \[y = \sqrt {x - 1} \].
So, the graph of \[y = \sqrt {x - 1} \] is given as follows:
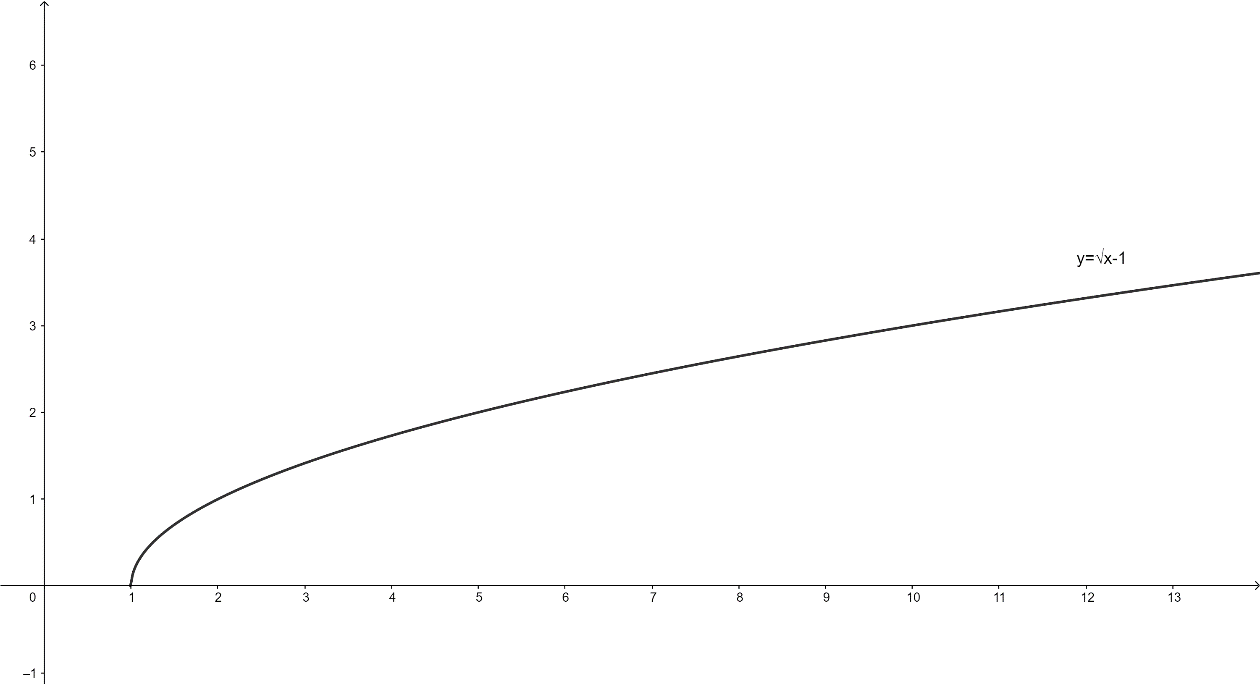
Now we will move the graph of \[y = \sqrt {x - 1} \] by \[3\] units down to obtain the graph of \[y = \sqrt {x - 1} - 3\].

Therefore, above graph is the required graph of \[y = \sqrt {x - 1} - 3\].
Here, the domain of \[y = \sqrt {x - 1} - 3\] is \[x \geqslant 1\] and range is \[y \geqslant - 3\].
Note:
Some rules to transform the given graph of a function that we should keep in mind are as follows:
\[(1)\] \[f(x + a)\] horizontally shifts the graph of \[f(x)\] to the left by \[a\] units.
\[(2)\] \[f(x - a)\] horizontally shifts the graph of \[f(x)\] to right by \[a\] units.
\[(3)\] \[f(x) + a\] vertically shifts the graph of \[f(x)\] upward by \[a\] units.
\[(4)\] \[f(x) - a\] vertically shifts the graph of \[f(x)\] downward by \[a\] units.
\[(5)\] \[af(x)\] vertically stretches the graph of \[f(x)\] by a factor of \[a\] units.
\[(6)\] \[\dfrac{{f(x)}}{a}\] vertically shrinks the graph of \[f(x)\] by a factor of \[a\] units.
\[(7)\] \[f(ax)\] horizontally shrinks the graph of \[f(x)\] by a factor of \[a\] units.
\[(8)\] \[f(ax)\] horizontally stretches the graph of \[f(x)\] by a factor of \[a\] units.
Complete step by step answer:
We have to graph \[y = \sqrt {x - 1} - 3\]. We can also write this as \[y - \left( { - 3} \right) = \sqrt {x - 1} \].
The parent function of the functions of the form \[f(x) = \sqrt {x - a} + b\] is \[f(x) = \sqrt x \].
Here, the domain of \[f(x) = \sqrt x \] is \[x \geqslant 0\] and the range is \[y \geqslant 0\].
We can graph \[y = \sqrt x \] as follows:

Now we will move the graph of \[y = \sqrt x \] by \[1\] unit to the right to obtain the graph of \[y = \sqrt {x - 1} \].
So, the graph of \[y = \sqrt {x - 1} \] is given as follows:
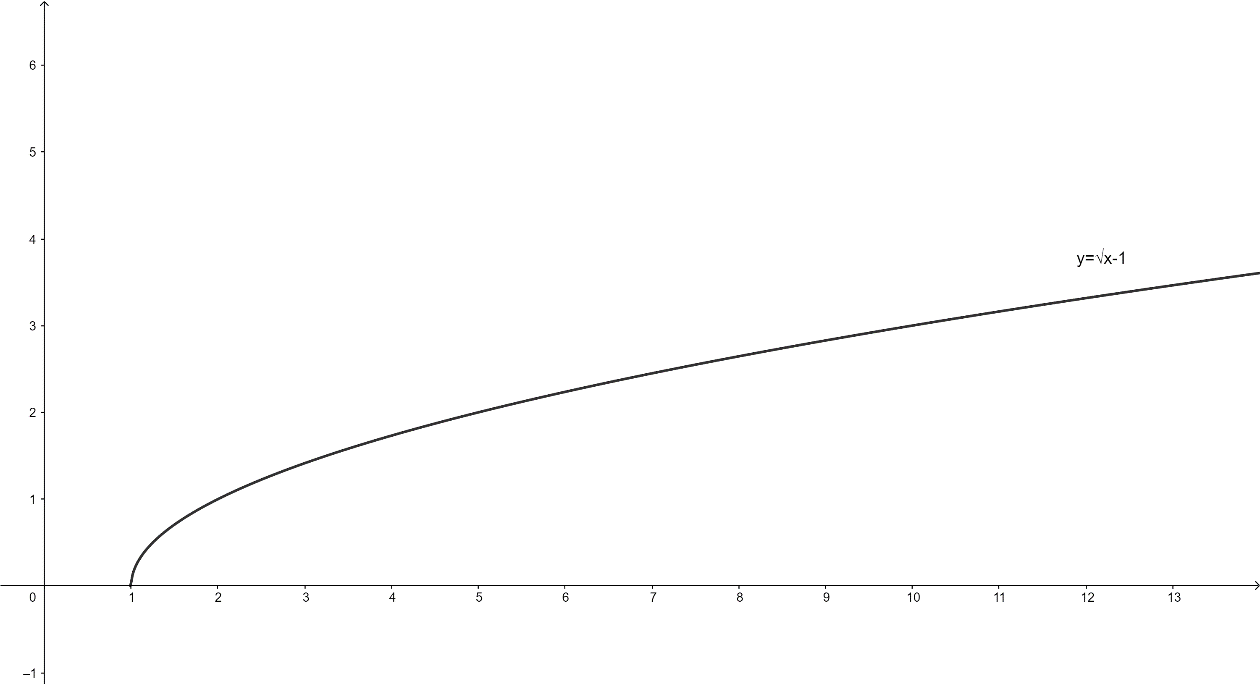
Now we will move the graph of \[y = \sqrt {x - 1} \] by \[3\] units down to obtain the graph of \[y = \sqrt {x - 1} - 3\].

Therefore, above graph is the required graph of \[y = \sqrt {x - 1} - 3\].
Here, the domain of \[y = \sqrt {x - 1} - 3\] is \[x \geqslant 1\] and range is \[y \geqslant - 3\].
Note:
Some rules to transform the given graph of a function that we should keep in mind are as follows:
\[(1)\] \[f(x + a)\] horizontally shifts the graph of \[f(x)\] to the left by \[a\] units.
\[(2)\] \[f(x - a)\] horizontally shifts the graph of \[f(x)\] to right by \[a\] units.
\[(3)\] \[f(x) + a\] vertically shifts the graph of \[f(x)\] upward by \[a\] units.
\[(4)\] \[f(x) - a\] vertically shifts the graph of \[f(x)\] downward by \[a\] units.
\[(5)\] \[af(x)\] vertically stretches the graph of \[f(x)\] by a factor of \[a\] units.
\[(6)\] \[\dfrac{{f(x)}}{a}\] vertically shrinks the graph of \[f(x)\] by a factor of \[a\] units.
\[(7)\] \[f(ax)\] horizontally shrinks the graph of \[f(x)\] by a factor of \[a\] units.
\[(8)\] \[f(ax)\] horizontally stretches the graph of \[f(x)\] by a factor of \[a\] units.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




