Question

Identical charges q each are placed at the eight corners of a cube of side b. Find the electrostatic potential energy of a charge +q placed at the center of the cube

Answer 1

Hint: First draw the diagram that is given in the question, then according to the question draw the diagonals and find the length of the diagonals in terms of side of a cube, the charge +q is placed at the center hence it means that the charge is at the center of the diagonals, find the point where charge +q is placed, now according to the formula for potential energy solve the question.

Complete step-by-step answer:

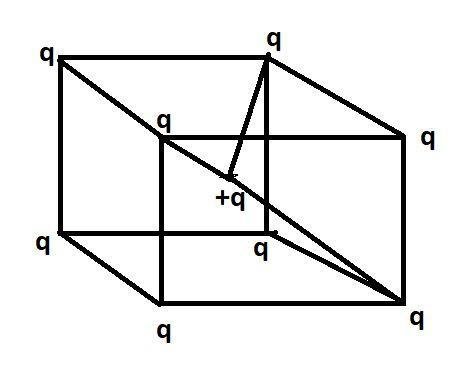
In this cube we see that there is a charge of q in all the corners and a charge +q is in the middle of the cube, in such a way that all the corners of the cube are at the same distance from the charge +q. We assume that the length of each side of the cube is b.
We know that length of the diagonal is = $\sqrt{3}\times sidelength$,
Which means=$\sqrt{3}\times b$
If we consider the distance between both the diagonal is l then= $\dfrac{\sqrt{3}\times b}{2}$
Now potential energy would be equal to,
$u=\dfrac{\sum k(q)(+q)}{l}$ ,here q and +q are two charges involved in the system, k is a constant, l is the point between the two diagonal.
Now as we have to find the potential energy for eight charges that are identical thus we can consider,
$u=\dfrac{8k({{q}^{2}})}{l}$,

$u=\dfrac{8\times 1\times ({{q}^{2}})}{4\pi {{\xi }_{\circ }}\left( \dfrac{\sqrt{3}}{2}b \right)}$,
Now on solving this,
\[u=\dfrac{4\times ({{q}^{2}})}{b\sqrt{3}\pi {{\xi }_{\circ }}}\]. (Answer)

Note: In the formula for potential energy we are calculating all the charges at once as they are identical charges and hence it will be easy for us to evaluate. The charge +q is at the center of the cube which means the distance of each of the charges at the corners is the same from charge +q.