Question

If a: b: c = 13: 5: 12, then prove that the triangle is right angled at A.

Answer 1

Hint: To solve this kind of question we will first try to eliminate the ratios and will try to convert all the variables a, b and c in the form of numbers and not in ratios. After doing so we will verify if a, b and c will satisfy Pythagoras theorem.

Complete step-by-step answer:
To solve this question, we use Pythagoras theorem which is stated as “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”. The hypotenuse is the longest side, as it is opposite to the angle 90°.

Given that a: b: c = 13: 5: 12 and we have to prove that the triangle is right angled triangle and also that it is right angled at A.

To solve this question, we first of all take x to be a common factor of the above given expression so as to convert all the ratio terms in number form and then by taking proper substitution of x in all of a, b and c we get,
a=13x, b=5x and c=12x

If the above sides a, b and c satisfy the criteria of Pythagoras theorem then the triangle obtained by a, b and c becomes right angled triangle.
To check we apply Pythagoras theorem on a=13x, b=5x and c=12x but before that we need to check for the hypotenuse.

Now, using and applying the fact that in Pythagoras theorem we have the biggest side as the hypotenuse, so we check for the biggest side in the given values of a, b and c.

After analysing we get that for a known value of x, a=13x is the biggest of all.
Therefore, we have a= 13x as the hypotenuse of the given right angled triangle.

Now applying Pythagoras theorem stated above on a, b and c we get,
\[{{a}^{2}}={{b}^{2}}+{{c}^{2}}\]

Substituting the values of a, b and c in the above expression we get,

\[\begin{align}
  & {{(13x)}^{2}}={{(5x)}^{2}}+{{(12x)}^{2}} \\
 & \Rightarrow 169{{x}^{2}}=25{{x}^{2}}+144{{x}^{2}} \\
 & \Rightarrow 169{{x}^{2}}=169{{x}^{2}} \\
\end{align}\]

Hence, we obtain that LHS is equal to RHS.
Also, we had hypotenuse at a=13x implies triangle ABC is right angled at A.
The figure can be obtained as below.

 

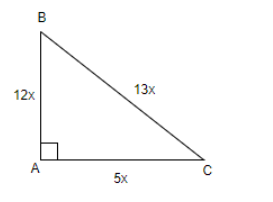
Therefore, the given triangle with sides a=13x, b=5x and c=12x is a right angled triangle at A.

Note:The possibility of error in the question can be not analysing which side will become the hypotenuse of the given triangle which will in turn make the solution or the answer incorrect because hypotenuse is the biggest side of all and Pythagoras theorem will not satisfy properly if we use any other side other than the hypotenuse itself.