Question

If a diagonal of a square is doubled, then the area of the square becomes m times. Find m.

Answer 1

Hint: Use Pythagoras theorem to find the diagonal of the square, then double it to get the new length. Use this length to compute the area of the resultant square.

Complete step by step answer:

Consider a square of side length ‘a’

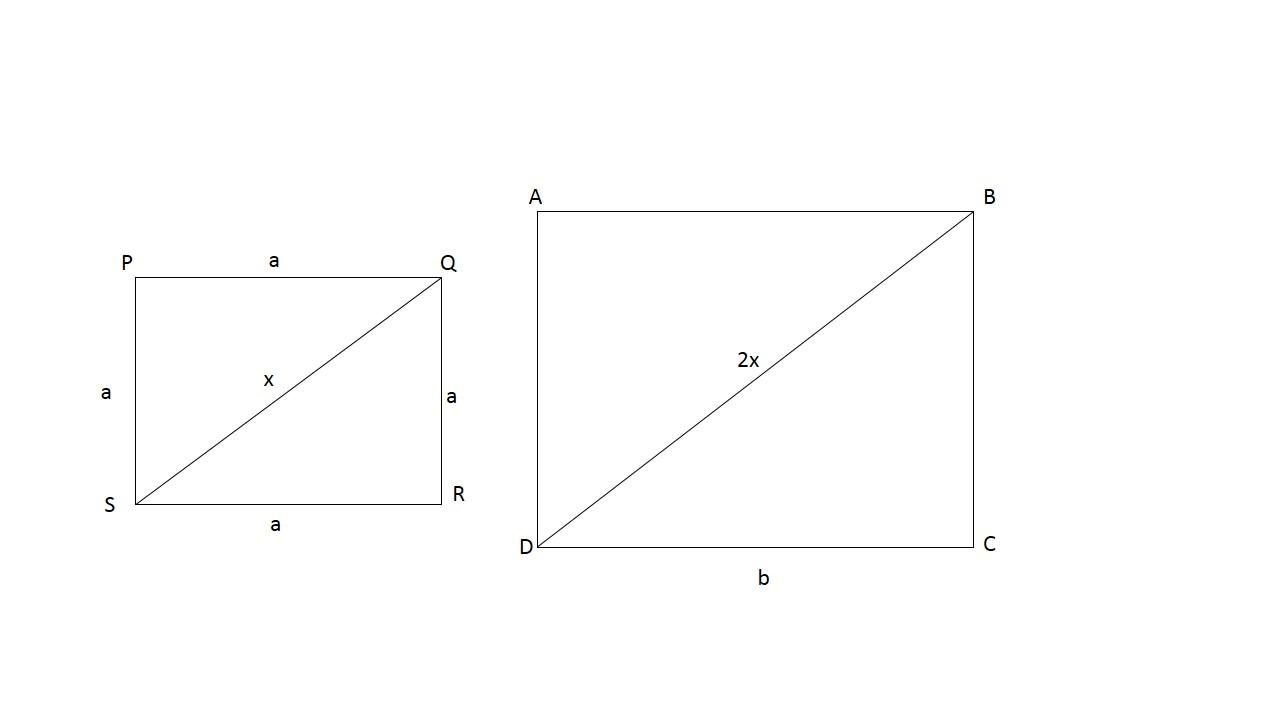
Using Pythagoras theorem on $\Delta \,\text{QRS}$,
     \[\begin{align}
  & \text{S}{{\text{R}}^{\text{2}}}\,\text{+}\,\text{Q}{{\text{R}}^{\text{2}}}\,\text{=}\,\text{Q}{{\text{S}}^{\text{2}}} \\
 & {{\text{a}}^{\text{2}}}\,\text{+}\,{{\text{a}}^{\text{2}}}\,\text{=}\,\text{Q}{{\text{S}}^{\text{2}}}
\end{align}\]
$\therefore $ length of diagonal $\text{QS}\,\text{=}\,\sqrt{\text{2}}\text{a}$
Now, according to the question, the diagonal of square
     \[\begin{align}
  & \text{ABCD}\,\text{=}\,\text{2 }\!\!\times\!\!\text{ }\,\text{diagonal}\,\text{of PQRS} \\
 & \text{=}\,\text{2}\,\times \,\sqrt{2}a \\
 & =\,2\sqrt{2}a.
\end{align}\]
Let us apply the Pythagoras theorem again on $\Delta \,\text{BCD}$
     \[\text{C}{{\text{D}}^{\text{2}}}\,\text{+}\,\text{B}{{\text{C}}^{\text{2}}}\,\text{=}\,\text{BD}\]
But $\text{BD}\,\text{=}\,\text{2}\sqrt{2}\text{a}$, as derived before
\[\begin{align}
  & \therefore \,\text{C}{{\text{D}}^{\text{2}}}\,\text{+}\,\text{B}{{\text{C}}^{\text{2}}}\,\text{=}\,\text{8}{{\text{a}}^{\text{2}}} \\
 & \text{But}\,\text{CD}\,\text{=}\,\text{BC}\,\text{=}\,\text{b}\,\text{(New square side)} \\
 & \text{2}{{\text{b}}^{2}}\,=\,8{{\text{a}}^{2}} \\
 & \text{b}\,\text{=}\,\text{2a}
\end{align}\]
So the new square has a side that’s double the length of the old square.
Let’s finally compare areas
     $\begin{align}
  & \text{Area}\,\text{of}\,\text{PQRS}\,\text{=}\,{{\text{a}}^{\text{2}}} \\
 & \text{Area}\,\text{of}\,\text{ABCD}\,\text{=}\,{{\text{b}}^{\text{2}}}\,\text{=}\,{{\text{(2a)}}^{\text{2}}}\,\text{=}\,\text{4}{{\text{a}}^{\text{2}}} \\
\end{align}$
     \[\therefore \,\dfrac{\text{Area}\,\text{of}\,\text{ABCD}}{\text{Area}\,\text{of}\,\text{PQRS}}\,\text{=}\,\dfrac{\text{4}{{\text{a}}^{\text{2}}}}{{{\text{a}}^{\text{2}}}}\,\text{=}\,\text{4}\]
Hence m = 4

Note: Remember that if a square changes its length by la times, its area changes by a factor of ${{\text{l}}^{2}}$, depending on whether the length is increase or decreases.
$\begin{align}
  & \text{If}\,\text{a}\,\to \,\text{la}\,\text{then}\,\text{area}\,\to \,{{\text{l}}^{\text{2}}}\,\text{area} \\
 & \text{If}\,\text{a}\,\to \,\dfrac{\text{l}}{\text{l}}\text{a}\,\text{then}\,\text{area}\,\to \,\dfrac{\text{l}}{{{\text{l}}^{\text{2}}}}\,\text{area} \\
\end{align}$