Question

If A is a subset of B, then which of the following is correct?
\[
  \left( A \right){A^c} \subseteq {B^c} \\
  \left( B \right){B^c} \subseteq {A^c} \\
  \left( C \right){A^c} = {B^c} \\
  \left( D \right)A \subseteq A \cap B \\
 \]

Answer 1

Hint: We solve this type of problem by using two methods . The first method is by taking an example and checking every option given in the problem and the second method is by using Venn diagrams .

Complete step-by-step answer:
The objective of the problem is to find the correct option from the given options.
This problem can be solved by two methods: they are verifying the options and the other one is by using Venn diagrams.
Method 1: By checking the given options
Given that A is the subset of B.
Let us consider the universal set denoted by U as \[U = \left\{ {a,b,c,d,e,f,g,h} \right\}\]
Let us consider the two sets A and B where A is the set of elements a,b,c,d and B is the set of elements a,b,c,d,e. The usual notation of sets A and B is \[A = \left\{ {a,b,c,d} \right\},\,B = \left\{ {a,b,c,d,e} \right\}\].
Now find A compliment and B complement.
\[{A^c}\]is defined as the set of all elements present in the universal set except the elements present in set A.
That is \[{A^c} = \left\{ {e,f,g,h} \right\}\]
Similarly , \[{B^c}\] is defined as the set of all elements present in the universal set except the elements present in the set B.
That is , \[{B^c} = \left\{ {f,g,h} \right\}\]
Now find the \[A \cap B\]. A intersection B is defined as the set of all elements that are common in the given two sets A and B.
That is \[A \cap B = \left\{ {a,b,c,d} \right\}\]
Now check the options given .First let us check option A .The option A is false because it is given that A is subset of B .Although the elements of \[{A^c}\] is contained in \[{B^c}\] the option is not satisfying the given if condition . Option B is true because the elements in \[{B^c}\] are contained in \[{A^c}\] and also satisfy the given condition. Similarly options C and D are also not correct .
Therefore, option B that is \[{B^c} \subseteq {A^c}\] is correct.
Method 2: By using Venn diagrams
The Venn diagram of \[A \subset B\] is

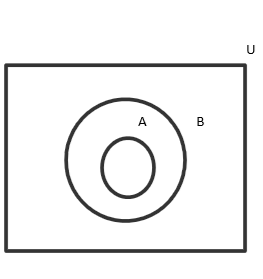
The Venn diagram for \[{A^c}\] is

The Venn diagram for \[{B^c}\] is

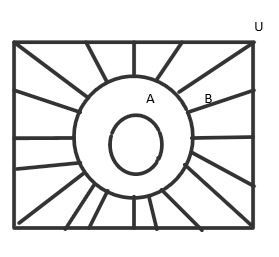
It is clear from the diagrams that \[{B^c} \subseteq {A^c}\].
Thus , option B is correct.


Note: Union is defined as the set of all elements that are contained in one and each other . A subset is defined as a set of which all the elements are contained in another set. Every set is subset to itself and the empty set is subset to every set.