Question

If a stands for the edge length of cubic system: simple cubic, body-centred cubic and face centred cubic, then the ratio of radii of radii of the spheres in these systems will be respectively:
A.$$\dfrac{1}{2}a:\dfrac{{\sqrt 3 }}{2}a:\dfrac{{\sqrt 2 }}{2}a$$
B.$$1a:\sqrt 3 a:\sqrt 2 a$$
C.$$\dfrac{1}{2}a:\dfrac{{\sqrt 3 }}{4}a:\dfrac{1}{{2\sqrt 2 }}a$$
D.$$\dfrac{1}{2}a:\sqrt 3 a:\dfrac{1}{{\sqrt 2 }}a$$

Answer 1

Hint: In a simple cubic unit cell, atoms are present at the corners. In a body-centred unit cell, atoms are present at the corners and one single atom is present at the body centre. In a face centred unit cell, atoms are present at the corners and as well as the six faces of the cell.
Step-by-step answer:
First we need to understand what atomic radius is. It is defined as half the distance between nearest neighbouring atoms in a crystal. It is expressed in terms of the length of the edge 'a' of the unit cell of the crystal.

In a simple cubic unit cell, atoms at the corner touch each other along the edge as shown below.

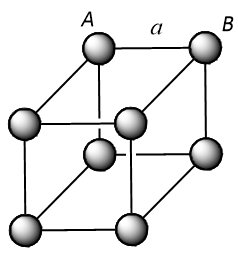
From the above structure, it can be concluded that the distance (d) between the nearest neighbours will be:
$$d = AB = a = 2r$$ (where, r is the radius of the atom)

Therefore, atomic radius (r) will become equivalent to:
$$r = \dfrac{a}{2}$$

Thus for a simple cubic unit cell, the radius of the sphere is equal to $$\dfrac{1}{2}a$$.

In a body-centred cubic unit cell, atoms are present at the corners as well as an atom is present at the body centre as shown below.

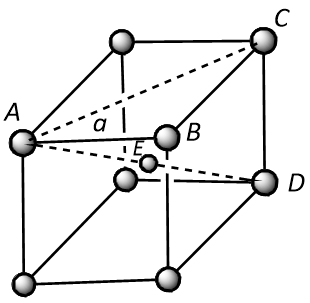
In the above structure, the distance between the two nearest neighbours is represented by length AE or ED that is half of the body diagonal, AD.

Thus it can be concluded that the distance (d) between the nearest neighbours will be:
$$d = AE = ED = \dfrac{{AD}}{2}$$ (where, r is the radius of the atom)

In $$\Delta ABC$$, the square of AC is equivalent to the sum of square of AB and square of BC. Thus it can be written as:
$$A{C^2} = A{B^2} + B{C^2}$$
Since it is clear from the structure that $$AB = BC = a$$

Therefore, we can write:
$$\displaylines{
  A{C^2} = {a^2} + {a^2} \cr
  A{C^2} = 2{a^2} \cr} $$

On squaring both sides, we get
$$AC = \sqrt 2 a$$

In $$\Delta ADC$$, the square of AD is equivalent to the sum of square of AC and square of CD. Thus it can be written as:
$$A{D^2} = A{C^2} + C{D^2}$$

Since it is clear from the structure that $$CD = a$$ and above we calculated $$AC = \sqrt 2 a$$. Thus substituting we get
$$\eqalign{
  & A{D^2} = {\left( {\sqrt 2 a} \right)^2} + {a^2} \cr
  & A{D^2} = 2{a^2} + {a^2} \cr
  & A{D^2} = 3{a^2} \cr} $$

On squaring both sides, we get
$$AD = \sqrt 3 a$$
Since it is clear from the above structure that the distance between two nearest neighbours is half of the diagonal AD. Thus, we can write:
$$d = \dfrac{{\sqrt 3 }}{2}a$$

Also we know that $$d = 2r$$. Thus
$$\displaylines{
  \dfrac{{\sqrt 3 }}{2}a = 2r \cr
  r = \dfrac{{\sqrt 3 }}{4}a \cr} $$

Thus for a body-centred unit cell, the radius of the sphere is equal to $$\dfrac{{\sqrt 3 }}{4}a$$.

In a face-centred cubic unit cell, atoms are present at the corners as well as faces of the unit cell. There are a total six faces in a cubic unit cell.

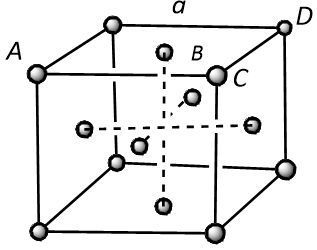
In the above structure, the distance between the two nearest neighbours is represented by length AB or BC that is half of the face diagonal, AC.

Thus it can be concluded that the distance (d) between the nearest neighbours will be:
$$d = AB = BC = \dfrac{{AC}}{2}$$ (where, r is the radius of the atom)

In $$\Delta ACD$$, the square of AC is equivalent to the sum of square of CD and square of AD. Thus it can be written as:
$$A{C^2} = C{D^2} + A{D^2}$$

Since it is clear from the structure that $$CD = AD = a$$

Therefore, we can write:
$$\displaylines{
  A{C^2} = {a^2} + {a^2} \cr
  A{C^2} = 2{a^2} \cr} $$

On squaring both sides, we get
$$AC = \sqrt 2 a$$

Since it is clear from the above structure that the distance between two nearest neighbours is half of the diagonal AC. Thus, we can write:
$$\displaylines{
  d = \dfrac{{\sqrt 2 }}{2}a \cr
   = \dfrac{1}{{\sqrt 2 }}a \cr} $$

Also we know that $$d = 2r$$. Thus
$$\displaylines{
  \dfrac{1}{{\sqrt 2 }}a = 2r \cr
  r = \dfrac{1}{{2\sqrt 2 }}a \cr} $$

Thus for a face-centred unit cell, the radius of the sphere is equal to $$\dfrac{1}{{2\sqrt 2 }}a$$.

The ratio of radii of spheres in simple cubic unit cell, body centred unit cell and face centred unit cell will be as:
$${\text{Ratio}} = \dfrac{1}{2}a:\dfrac{{\sqrt 3 }}{4}a:\dfrac{1}{{2\sqrt 2 }}a$$

Therefore, the correct option is C.

Note: While doing such a question, we do not need to derive the whole radius of the atom. We just need to remember the formula of radius for each system.
For a simple cubic unit cell, $$r = \dfrac{a}{2}$$.
For a body-centred unit cell, $$\dfrac{{\sqrt 3 }}{4}a$$.
For a face-centred unit cell, $$\dfrac{1}{{2\sqrt 2 }}a$$.