
If ABC is an obtuse triangle with
Answer
451.2k+ views
Hint: According to the given question we have to find the measure of obtuse angle
Obtuse angle: An obtuse angle is the angle which is more than
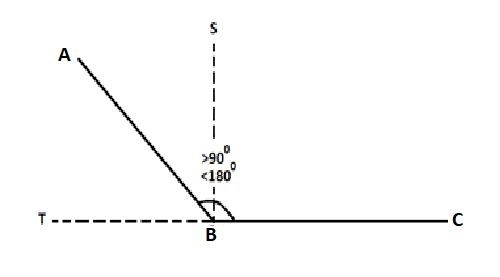
As we can see in the diagram given above,
Complete step-by-step solution:
Given,
Measures of
Now, we have to measure the obtuse angle
Obtuse triangle: An obtuse triangle is the triangle in which it’s one interior angle measure is more than the
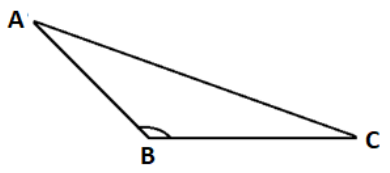
Hence, for the given triangle ABC,
Step 1: To measure the obtuse angle
We have to let that the given obtuse angle is
Step 2: As we know, the sum of all the interior angles of a triangle is
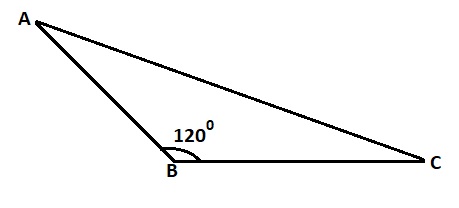
Step 3: As we let that an obtuse angle
So, measure of
Hence, we can say that for a obtuse triangle ABC, obtuse angle
Note:
1. The side opposite to the obtuse angle is the longest side for that given triangle.
2. An equilateral triangle can’t be an obtuse triangle because it’s all sides are equal in size and it’s all the interior angles are
3. A triangle can’t be right-angled and obtuse angled at the same time. Since a right angle has one right angle and the other two interior angles are acute.
Obtuse angle: An obtuse angle is the angle which is more than

As we can see in the diagram given above,
Complete step-by-step solution:
Given,
Measures of
Now, we have to measure the obtuse angle
Obtuse triangle: An obtuse triangle is the triangle in which it’s one interior angle measure is more than the

Hence, for the given triangle ABC,
Step 1: To measure the obtuse angle
We have to let that the given obtuse angle is
Step 2: As we know, the sum of all the interior angles of a triangle is

Step 3: As we let that an obtuse angle
So, measure of
Hence, we can say that for a obtuse triangle ABC, obtuse angle
Note:
1. The side opposite to the obtuse angle is the longest side for that given triangle.
2. An equilateral triangle can’t be an obtuse triangle because it’s all sides are equal in size and it’s all the interior angles are
3. A triangle can’t be right-angled and obtuse angled at the same time. Since a right angle has one right angle and the other two interior angles are acute.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹31,500 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




